ΠΤΥΧΩΣΗ - ΠΤΥΧΕΣ - ΔΥΝΑΜΙΚΗ ΑΝΑΛΥΣΗ ΠΤΥΧΩΝ

 

ΠΤΥΧΩΣΗ ΠΤΥΧΕΣ

(επισημάνσεις)

ΔΥΝΑΜΙΚΗ ΑΝΑΛΥΣΗ ΠΤΥΧΩΝ

(εξίσωση Biot-Ramberg, αριθμός Deborah )

απαιτούνται γνώσεις Τεκτονικής Γεωλογίας

ΠΤΥΧΩΣΗ – ΠΤΥΧΕΣ

Ορισμοί:

Με τον όρο πτυχή (fold) εννοούμε την τεκτονική δομή, η οποία αρχικά, σε αλλεπάλληλες στρώσεις επιπέδων επιφανειών όπως τα ιζηματογενή πετρώματα, προκαλεί κύρτωση (bend) ή κάμψη (buckle) ως αποτέλεσμα πλαστικής – όλκιμης παραμόρφωσης. Απαντώνται ως απλές απομονωμένες πτυχές μέχρι και εκτεταμένες ακολουθίες πτυχών (fold trains) σε όλες τις κλίμακες μεγέθους. Ομάδα πτυχών κατανεμημένη σε τοπική κλίμακα απαρτίζει μια πτυχωγενή ζώνη, η οποία συνήθως συνδέεται με συγκλίνοντα όρια πλακών και με άμεση συμπιεστική τάση.

Πτύχωση (folding) είναι μία έννοια η οποία συμπεριλαμβάνει όλες τις γεωλογικές διεργασίες με τις οποίες επιφάνειες πετρωμάτων κάμπτονται κατά την στρεβλωτική παραμόρφωση (strain). Εφόσον οι πτυχές είναι μόνιμα παραμορφωμένες δομές με καθόλου ή ελάχιστη απώλεια της συνοχής των πτυχωμένων στρωμάτων, η πτύχωση κατ’ ουσία, αναφέρεται σε αργή όλκιμη ελαστική συμπεριφορά των μαλακών ή/και θερμών πετρωμάτων. Διαφορετικοί μηχανισμοί πτυχώσεων, που έχουν συνδυάσει μερικές βασικές διεργασίες καταδεικνύουν, τις γεωμετρικές (πάχος στρωμάτων και η μεταξύ τους απόσταση) και φυσικές (ιξώδες, διαφορές ιξωδών, ανισοτροπία) ιδιότητες των πετρωμάτων. 

Θα πρέπει να σημειωθεί ότι η τάση (stress) από μόνη της είναι ανεπαρκής να δημιουργήσει πτύχωση καθώς θα πρέπει πρώτα να υπάρχουν επιφάνειες επίπεδων ώστε να καθοριστεί το σχήμα της πτυχής καθώς επίσης και ο προσανατολισμός των επιπέδων σε συνάρτηση με τη διεύθυνση της τάσης, η οποία, καθορίζει με πολλούς τρόπους το είδος της προκύπτουσας πτυχής.

Βασικά γεωμετρικά στοιχεία πτύχωσης.

η

Γενικά οι πτυχές απαρτίζονται από μία άρθρωση (hinge) οποία συνδέει δυο διαφορετικού προσανατολισμού σκέλη (limbs). Η άρθρωση μπορεί να είναι αιχμηρή ή τραχύς συνήθως με βαθμιαία καμπυλότητα καθαρίζοντας έτσι μια ζώνη άρθρωσης (hinge zone). Λόγω της μαθηματικής μορφής που παρουσιάζουν οι πτυχές μπορούμε να ορίσουμε εύρος (amplitude) και μήκος κύματος. Σημείο άρθρωσης (hinge point) είναι το σημείο της μεγίστης καμπυλότητας ενός πτυχωμένου στρώματος και εντοπίζεται στο κέντρο της ζώνης άρθρωσης. Η συνένωση των εν λόγω σημείων, σε τρεις διαστάσεις, ορίζει την γραμμή άρθρωσης (hinge line). Πτυχές με ευθείες γραμμές άρθρωσης είναι κυλινδρικές. Η αξονική επιφάνεια (axial surface) ή αξονικό επίπεδο (axial plane) - κατά προσέγγιση επίπεδο – συνδέει τις γραμμές άρθρωσης δύο ή περισσοτέρων πτυχωμένων επιφανειών.

Αντίμορφο – Σύνμορφο: Οι αντίστοιχοι όροι αντίκλινο και σύγκλινο έχουν στρωματογραφική έννοια. Τα αντίκλινα έχουν παλαιότερη στρωμάτωση στον πυρήνα, ενώ τα σύγκλινα νεώτερη. Υπάρχουν περιπτώσεις αντίμορφου σύγκλινου και σύνμορφου αντίκλινου σε επαναπτυχώμενες περιοχές. Σ’ αυτές το σημαντικότερο είναι να προσδιορισθεί η κατεύθυνση της νεώτερης στρωμάτωσης κατά μήκος του αξονικού επιπέδου. 

Διαδικασίες πτύχωσης.

Σε αρκετά μοντέλα σχηματισμού πτυχών δεν λαμβάνονται υπόψη οι δυνάμεις αντιστάσεις του σώματος καθώς και η επίδραση των υλικών τα οποία περιβάλλουν τα στρώματα (και τα δύο αντιμετωπίζονται ως παχύρευστα υγρά). Έχουν, όμως, καθοριστικό ρόλο στον προσδιορισμό ή στην τροποποίηση της γεωμετρίας της πτυχής. Επίπεδα στρώματα μπορούν να καμφθούν με αρκετούς τρόπους:

Περιστροφή

Είναι προφανές ότι η πτύχωση περιστρέφει τα μέρη των στρωμάτων και ως εκ τούτου η συνεχής αλλαγή στον προσανατολισμού των σκληρών στρωμάτων, ως προς την κατεύθυνση της βράχυνσης, προκαλεί αρχικά σημαντική μείωση της συμπιεστικής αντίστασης του πετρώματος. Αυτή είναι μία μορφή εξασθένισης του συνολικού όγκου του πετρώματος, η οποία συνοδεύεται από προοδευτική τροποποίηση της εσωτερικής γεωμετρίας του χωρίς μεταβολές στις ιδιότητές του (πχ. ιξώδες). Και συνεπώς ονομάζεται δομικό μαλάκωμα (structural softening), το οποίο ακολουθείται από μία αύξηση στην συμπιεστική αντίσταση, την δομική σκλήρυνση (structural hardening). Μαλάκωμα και σκλήρυνση είναι οι προϋποθέσεις για την εμφάνιση της ανάπτυξης και αλλοίωσης της αστάθειας του συστήματος.

Επιμήκυνση

Οι αρθρώσεις των πτυχών συχνά καθορίζουν τη θέση όπου οι πτυχές ξεκινούν να αναπτύσσονται, συνήθως σε μικρή απόσταση, έτσι ώστε κάθε άξονας της πτυχής να προωθείται προς τα άκρα των τμημάτων των αρθρώσεων. Περαιτέρω περιστροφή των σκελών με την επακόλουθη κατά μήκος ανάπτυξη της πτυχής, δεν συνδέεται με συμμετρική μετακίνηση των άκρων των αρθρώσεων.

Μηχανική των στρωμάτων: Ενεργητική / παθητική πτύχωση

Κάθε παραμόρφωση συνεπάγεται μετατόπιση των υλικών σωματιδίων. Ένα παθητικό σωματίδιο δεν αλληλοεπιδρά με τα γειτονικά του, παρά μόνο κινείται. Αντίθετα, ένα ενεργό σωματίδιο αλληλοεπιδρά με τα γειτονικά του και η μετακίνησή του επηρεάζεται από αυτήν των γειτονικών του σωματιδίων.

Στην γεωλογία, η σύνθετη στρωμάτωση έχει μηχανικές ιδιότητες οι οποίες επηρεάζουν το πρότυπο παραμόρφωσης κατά την διαδικασία της πτύχωσης. Για παράδειγμα, περιθώρια μεταξύ στρωμάτων με διαφορά αντοχής (ιξώδους), ολισθαίνουν ή υφίστανται τοπική διατμητική παραμόρφωση, γεγονός που προσδιορίζει το πως θα αναπτυχθούν οι καμπυλότητες.

Η πτύχωση είναι ενεργητική όταν η παραμόρφωση λαμβάνει χώρα σε κλίμακα στρωμάτων, και η διαφορά αντοχής (strength) μεταξύ των στρωμάτων επιδρά άμεσα στο πρότυπο της μεταμόρφωσης. Αντίστροφα, η παθητική πτύχωση λαμβάνει χώρα σε κλίμακα κόκκου, καθώς τα στρώματα δεν έχουν σημαντική διαφορά ανθεκτικότητας και ως εκ τούτου δεν παράγουν τάση που να εφαρμόζεται κατά μήκος και/ή παράλληλα με τα περιθώρια των στρωμάτων. Σ’ αυτή την περίπτωση η στρωμάτωση χρησιμεύει απλώς ως γεωμετρικός δείκτης παραμόρφωσης.

O John Ramsey παρουσίασε μια γεωμετρική ταξινόμηση των πτυχών ως προς τις κλίσεις των ισογωνίων. Προσανατολίζοντας την πτυχή έτσι ώστε το αξονικό επίπεδο να είναι κάθετο, μπορούμε να φέρουμε, από το εξωτερικό και εσωτερικό περιθώριο της πτυχής, γραμμές μεταξύ σημείων όμοιας κλίσης. Με αυτό τον τρόπο φαίνεται η διαφορά μεταξύ των περιθωρίων και επομένως οι αλλαγές στο πάχος των στρωμάτων. Έτσι οι πτυχές ταξινομούνται σε τρεις κατηγορίες – τάξεις (class):

Τάξη 1: Οι κλίσεις των ισογωνίων συγκλίνουν προς το εσωτερικό τόξο το οποίο είναι παχύτερο από αυτό του εξωτερικού.

Τάξη 2 ή όμοιες διατμητικές πτυχές: Οι κλίσεις των ισογωνίων είναι παράλληλες ως προς τον άξονα του κάθετου επιπέδου και το σχήμα του εσωτερικού και εξωτερικού τόξου είναι ίδιο.

Τάξη 3: Οι κλίσεις των ισογωνίων αποκλίνουν προς το εσωτερικό τόξο το οποίο είναι πιο «ανοικτό» από το εξωτερικό.

Η Τάξη 1 των πτυχών υποδιαιρείται στην:

Τάξη 1Α οι οποίες χαρακτηρίζονται από λεπτές ζώνες άρθρωσης, στην

Τάξη 1Β οι όποιες ονομάζονται και παράλληλες πτυχές και στην

Τάξη 1C οι οποίες έχουν λεπτότερα σκέλη. 

Παθητική πτύχωση (πτυχές Τάξης 2)

Η παθητική πτύχωση συναντάται σε πετρώματα που παρατηρείται παθητική ροή δηλ. στη στρωμάτωση δεν εφαρμόζεται μηχανισμός ώστε να επηρεάζει την πτύχωση και καλείται παθητική στρωμάτωση καθώς μεταξύ των στρωμάτων δεν υπάρχει διαφορά ανθεκτικότητας. Η προκύπτουσα πτύχωση δημιουργεί παθητικές πτυχές Τάξης 2 με απλή διάτμηση, όμοιες ή διατμητικές οι οποίες σχηματίζονται σε οποιοδήποτε καθεστώς όλκιμης παραμόρφωσης δηλ. σε υποαπλή (subsimple) διάτμηση, σε διασυμπίεση (transpression) και ακόμη σε ομοαξονική στρεβλωτική παραμόρφωση (coaxial strain) εξ ου και διατμητικές (shear folds). Οι πτυχές αυτές ονομάζονται και αρμονικές καθώς η στρωμάτωση δεν επηρεάζει την πτύχωση και επομένως το σχήμα της πτυχής.

Κύρτωση (bending)-

Η κύρτωση παρατηρείται όταν δυνάμεις ασκούνται εγκάρσια με μεγάλη γωνία ως προς τα στρώματα, όπως πχ η υπερφόρτιση ραφιών βιβλιοθήκης και οφείλονται σε έναν ή και περισσότερους μηχανισμούς. Πάντως μπορεί να θεωρηθεί και ως παθητική πτύχωση καθώς με την κύρτωση συνδέονται στενά.

Κύρτωση (bending)- παθητική πτύχωση

Κυρτώσεις κλίμακας λιθόσφαιρας.

Οι πτυχές αυτή της κλίμακας που δημιουργούνται από κύρτωση είναι κοινές στους κράτωνες όπου κάθετες τάσεις σχηματίζουν μεγάλους θόλους, λεκάνες, υπερυψώσεις και ταπεινώσεις στα αρχικά οριζόντια επίπεδα. Κυρτώσεις στις λιθοσφαρικές πλάκες λαμβάνουν χώρα, ακόμη, στις ζώνες υποβύθισης και στις παρακείμενες ωκεάνιες ράχες, καθώς επίσης σε  μικρότερες συγκεντρώσεις των ηφαιστειογενών ωκεάνιων σχηματισμών όπως στα guyots (πχ. Χαβάη) και εκεί όπου  δημιουργούνται φορτία παγου ή ιζημάτων τα οποία υποβάλλουν τη λιθόσφαιρα σε ανακατάταξη των πτυχών. Ακόμη τέτοιες κυρτώσεις αναπτύσσονται στις λεκάνες της προχώρας, που είναι παρακείμενες στα ορογενή συστήματα. Η τάση που προέρχεται από τη βαρύτητα θεωρείται σημαντική κατά την κύρτωση σε κλίμακα λιθόσφαιρας.

Κυρτώσεις κλίμακας φλοιού.

Οι κυρτώσεις εδώ δημιουργούνται με ήπιες παλινδρομικές στρεβλώσεις. Παραδείγματα αποτελούν  οι κυρτωμένες καλύψεις των πετρωμάτων πάνω από  εισχωρούντες πλουτωνίτες; με τον σχηματισμό  παρελκτικών (drag), συρόμενων (drape) και εξαναγκαστικών (forced) πτυχών.

Οι παρελκτικές πτυχές (drag folds) είναι τοπικές κάψεις σε ζώνες ρηγμάτων. Συνήθως κυρτώνουν προς τη διεύθυνση κίνησης του ρήγματος η οποία αποδίδεται σε κάποια αντίσταση τριβής που εμποδίζει τη ολίσθηση κατά μήκος του ρηγματικού πεδίου. Αυτή η ερμηνεία προτείνει ότι η ρηγμάτωση ξεκίνησε πρώτη και ότι η πτύχωση σχηματίζεται στα παρακείμενα ρήγματα, όπου ένα τέμαχος περέλκεται κατα μήκος άλλου.

Οι συρόμενες πτυχές (drape folds) είναι ασύμμετρες, σχηματιζόμενες με διαφορικές κινήσεις σε ασθενείς επιφάνειες πιο ανθεκτικών πετρωμάτων και συνήθως παρουσιάζονται στα σκέλη μεγαλύτερων πτυχών ως τυπικές μονοκλινείς δομές.

Οι εξαναγκαστικές πτυχές (forced fold), κλασσικό γεωλογικό αποτέλεσμα της κύρτωσης, σχηματίζονται όταν ιζήματα τα οποία καλύπτουν ένα σκληρό υπόβαθρο και κινούνται κατά μήκος ρηγμάτων ακανόνιστου σχήματος. Πάνω από κανονικό ρήγμα η κύρτωση των στρωμάτων προκαλεί παράλληλη επέκταση, ενώ πάνω από ανάστροφο προκαλεί καμπτική επιφάνεια.

Σεισμικές μετρήσεις δείχνουν ότι οι εξαναγκαστικές πτυχές είναι τυπικές ασύμμετρες μονοκλινείς με μακρά, ελαφρώς κυρτά τα πίσω σκέλη και με κοντά, μεγάλης κλίσης τα εμπρόσθια, προς την φορά κίνησης των ιζημάτων, καλύπτοντας επίπεδες ή καμπύλες επιφάνειες υποβάθρου των πετρωμάτων, (Prucha et al. 1965, Steams 1971, Reches 1978, Stone 1983, 1985, Schmidt et al. 1993). Η εξαναγκαστική πτύχωση θεωρήθηκε ως ο κύριος μηχανισμός αυτών των δομών, με ουσιώδες χαρακτηριστικό του την παθητική παραμόρφωση των ιζηματογενών καλυμμάτων και την μετατόπιση των σκληρών πετρωμάτων σε κανονικά και λιστρικά ρήγματα, (Reches and Johnson 1978, Steams 1978).

Ερευνητές, για την περιγραφή των εξαναγκαστικών πτυχών χρησιμοποίησαν κινηματικά και γεωμετρικά μοντέλα κοινής χρήσης στην Τεκτονική Γεωλογία. Για τον παράλληλο, ως προς το υπόβαθρο, σχηματισμό γωνιακής οξύληκτης (kink) πτύχωσης, oι Narr and Suppe (1994) υπέθεσαν ότι το μήκος του υποστρώματος και η περιοχή της διατομής διατηρούνται, ώστε το πάχος του υποστρώματος και η κύρτωση των σκελών να είναι ομοιόμορφη (σχήμα Β) .

Οι Mitra and Mount (1998) θεώρησαν ότι οι εν λόγω πτυχές σχηματίζονται πάνω από ρήγματα που αποτελούνται από «συνδεδεμένα» ευθεία τμήματα και εισηγήθηκαν δύο περιπτώσεις σχηματισμού (σχήμα C, D): ως προς τη δόμηση του υποβάθρου, με κριτήριο από το αν το κάλυμμα του πετρώματος είναι συγκολλημένο (welded) στο υπόβαθρο ή αποκολλημένο (detachment) απ’ αυτό. Υπέθεσαν ακόμη, διαισθητικά, ότι η παραμόρφωση, στην πρώτη περίπτωση (συγκόλληση) θα πρέπει να είναι επικεντρωμένη σε τριγωνική ζώνη και σε ορθογώνια αν είναι αποκολλημένη.

Ο Erslev (1991), εισηγήθηκε ένα τρισδιατμητικό κινηματικό μοντέλο (σχήμα Α), το οποίο παράγει πιο ρεαλιστικές γεωμετρίες πτύχωσης με στρογγυλεμένες αρθρώσεις και μεταβαλλόμενες γωνίες κύρτωσης των σκελών.

Να σημειωθεί ότι οι εξαναγκαστικές πτυχές μπορούν να αναπτυχθούν σε κάθε τεκτονικό περιβάλλον και είναι εξίσου κοινές σε εκτατικά και συμπιεστικά εντατικά πεδία. Ο κύριος μηχανισμός είναι πάντα ή κύρτωση.

Άλλες πτυχές φλοιού είναι αυτές του καπτόμενου ρήγματος (fault-bend folds) οι οποίες σχηματίζονται από παθητική κύρτωση ενός εκτατικού επιπέδου πάνω σε ράμπα. Τέτοιες πτυχές είναι μάλλον οι μοναδικές από τις πτυχές κύρτωσης που σχηματίζονται σε ορογενείς ζώνες από τεκτονικές δυνάμεις.

Κάμψη (buckling)-ενεργητική πτύχωση Τάξης 1Β.

Η κάμψη είναι μια διαδικασία πτύχωσης η οποία ξεκινά όταν ένα στρώμα βραχύνεται παράλληλα με την στρωμάτωση δεδομένου ότι απαιτείται διαφορά ιξώδους, δηλαδή όταν μία ανθεκτική στρωμάτωση (πχ στρώμα χαμηλού βαθμού εύπλαστης ροής) εγκλείεται σε μη ανθεκτικά σώματα (υψηλού βαθμού εύπλαστης ροής).Η παρουσία στρωμάτων επαρκούς διαφοράς ιξώδους, παράγει μηχανική ανισοτροπία, η οποία είναι απαραίτητη για την κάμψη, ούτως ώστε το αδύναμο περιβάλλον υλικό να γεμίζει τα κενά των ισχυρών πτυχωμένων στρωμάτων. Τέτοιες καταστάσεις είναι γεωλογικά συνήθεις καθώς έτσι εξηγείται η συχνότητα εμφάνισης πτυχών κάμψης. Ακόμη με την κάμψη αναπτύσσονται στρογγυλευμένες πτυχές παράλληλες με περίπου ημιτονοειδές σχήμα.

Καπτώσεις απλού στρώματος.

Οι καπτώσεις απλών στρωμάτων είναι κοινές στη φύση, όπως για παράδειγμα ένα απομονωμένο επίπεδο ψαμμίτων ή ασβεστόλιθων σε μία παχιά ακολουθία  σχιτοπηλών,  ή σε φλέβες  πυριγενών πετρωμάτων που εισχώρησαν σε μη-στρωματοποιημένα επίπεδα. Το καπτώμενο στρώμα διατηρεί το πάχος του καθ’ ολοκληρία, σχηματίζοντας έτσι μία παράλληλη συγκεντρική πτυχή, οι οποία, πειραματικά, είναι συνήθως συμμετρική.

Πολυστρωματικές κάμψεις.

Μια πολυστρωμάτωση είναι ένα «πακέτο» διαφορετικών στρωμάτων και αποτελούν την πλέον κοινή κατάσταση στη Γεωλογία, όπως μια ιζηματογενής διαδοχή αποτελεί συχνά μια ομαλή μεταβολή μεταξύ δύο ή τριών τύπων πετρωμάτων (πχ. ψαμμίτες και σχιστοπηλοί σε τουρβιδίτες).

Τα εναλλασσόμενα στρώματα έχουν μεταβαλλόμενο πάχος και ανθεκτικότητα. Θεωρητικές και πειραματικές μελέτες έδειξαν ότι η συμπεριφορά των πολυστρωμάτων εξαρτάται από ένα αριθμό παραγόντων, π.χ. η ποσότητα και το πάχος των ανθεκτικών στρωμάτων, η μεταξύ των απόσταση και η διαφορά ανθεκτικότητας μεταξύ των στρωμάτων και μεταξύ του περικλείοντος αυτών υλικού.

Σε ακολουθίες πολυστρωμάτων με ανομοιογενές πάχος και ιξώδες έχουν περιγραφεί δύο πιθανά διαφορετικά μοντέλα, τα οποία εξαρτώνται από την απόσταση μεταξύ των ανθεκτικών στρωμάτων:

1) Αν η μεταξύ τους απόσταση είναι μεγάλη (μεγαλύτερη από το επικρατούν μήκος κύματος (W_d), το οποίο είναι θέμα της δυναμικής της πτύχωσης και αναλύεται παρακάτω), η πολυστρωμάτωση συμπεριφέρεται μηχανικά ως σειρά απλών στρωμάτων. Κάθε ανθεκτικό στρώμα τείνει να κάμπτεται ως ένα ανεξάρτητο στρώμα πτύχωσης σύμφωνα με τη θεωρία του απλού στρώματος. Επομένως, παχύτερα στρώματα παρουσιάζουν ένα μεγαλύτερο μήκος κύματος από ότι τα λεπτότερα. Αυτή η εκδοχή έχει ως αποτέλεσμα την «δυσαρμονική πτύχωση». Πτυχές με μικρότερο μήκος κύματος και εύρος (παρασιτικές πτυχές) μπορούν να αναπτυχθούν, με αυτή τη διαδικασία, σε διάφορα μεγέθη εντός των (μεγα-) πτυχών της πολυστρωμάτωσης.

2) Αν οι αποστάσεις είναι μικρές (≥ 1/Wd), τα ανθεκτικά στρώματα μπορούν να παρεμβάλλονται μεταξύ των. Συχνά, τα δυνατότερα (ή παχύτερα) στρώματα με το μεγαλύτερο μήκος κύματος υπερτίθενται σ’ αυτά με το μικρότερο μήκος κύματος, τα λιγότερο ανθεκτικά και/ή λεπτότερα.

Η πολυστρωματικότητα συμπεριφέρεται μηχανικά ως μία ενιαία στρωμάτωση καθώς όλα τα στρώματα προσαρμόζονται στο ίδιο μήκος κύματος, το οποίο συνήθως επιβάλλεται από αυτό του  δυνατότερου και παχύτερου στρώματος Υπάρχει μία μηχανική αλληλεπίδραση μεταξύ των ανθεκτικών και μη ανθεκτικών στρωμάτων. Η πτύχωση είναι αρμονική* ακόμη και όταν τα ανθεκτικά στρώματα είναι τόσο κοντά το ένα στο άλλο ώστε η πολυστρωμάτωση συμπεριφέρεται ως ένα ανισότροπο στρώμα, η οποία θα καμφθεί σύμφωνα με τον λόγο του μικρότερου μήκος κύματος ως προς το πάχος, απ’ ότι ένα ισότροπο στρώμα με το ίδιο πάχος.

*[Αρμονικές είναι οι πτυχές οι οποίες σε πολυστρωματικά πετρώματα επαναλαμβάνονται με το ίδιο σχήμα και προς την διεύθυνση του άξονα.]

Στην παραπάνω εικόνα φαίνεται ότι οι μεγαλύτερες πτυχές επηρεάζουν την όλη πολυστρωμάτωση.

Σε πολυστρωματικό σύμπλεγμα, αναπτύσσονται πτυχές διαφορετικού μήκους κύματος και κάποιες απ’ αυτές αυξάνονται με διαφορετικές αναλογίες μεταξύ των. Μπορεί να αλληλο-παρεμβάλλονται και συχνά ένα μεγαλύτερο μήκος κύματος υπερτίθεται σε μικρότερο, διότι το μη ανθεκτικό στοιχείο προσαρμόζεται με τις αλλαγές του σχήματος οι οποίες υπαγορεύεται από την κάμψη του δυνατότερου στρώματος. Έτσι, πτυχές διαφορετικών βαθμίδων αναπτύσσονται από αυτή την παρεμβολή.

Οι διαφορετικοί τύποι καμπτικής συμπεριφοράς εξηγούνται λαμβάνοντας υπόψη την παραμόρφωση στο περιβάλλον σώμα (matrix), γύρω από ένα από ανθεκτικό στρώμα καθώς αυτό κάμπτεται. Το σώμα εκτοπίζεται από την αναπτυσσόμενη πτυχή, αλλά αυτή η μετατόπιση σταδιακά εξαφανίζεται από το πτυχώμενο στρώμα και θεωρείται αμελητέα σε μια απόσταση περίπου ίση με του επικρατούντος μήκους κύματος.

Η ζώνη ετερογενούς διατάραξης (παραμορφωτική πτύχωση) σε κάθε πλευρά του καπτόμενου στρώματος είναι γνωστή ως ζώνη επαφής παραμόρφωσης (ΖΕΠ: zone of contact strain). Αν τα ανθεκτικά στρώματα βρίσκονται σε σημαντική απόσταση μεταξύ των, τότε δεν υπάρχει επικάλυψη των ΖΕΠ και κάθε στρώμα κάμπτεται σαν να είναι απλό.

Αντίθετα, αν οι ΖΕΠ των παρακείμενων στρωμάτων επικαλύπτονται τότε δεν είναι πλέον δυνατό τα στρώματα να κάμπτονται ανεξάρτητα το ένα από το άλλο. Επιπλέον, οι συσχετιζόμενες ΖΕΠ των παρακείμενων στρωμάτων, πρέπει να είναι συμβατές και ως εκ τούτου, όλα τα στρώματα προσαρμόζονται στο ίδιο παραμορφωτικό πεδίο αναπτύσσοντας το ίδιο μήκος κύματος.

Με σκοπό να καθορίσουμε πόσο κοντά πρέπει να είναι τα ανθεκτικά στρώματα για να θεωρηθούν ως πολυστρωμάτωση, σε αντίθεση με την κάμψη απλού στρώματος, είναι αναγκαίο να γνωρίζουμε πόσο μακριά η ΖΕΠ μπορεί να επεκταθεί από το στρώμα εντός του σώματος που το περιβάλλει. Έτσι για ένα ιξώδες σώμα, η διατάραξη στη ΖΕΠ θα πρέπει να «σβήσει», περίπου, στο 1% από τη μεγίστη τιμή της και σε απόσταση όσο το μήκος κύματος από την κάθε πλευρά του καπτόμενου στρώματος. 

Καμπτική πτύχωση από διασύνδεση.

Η καμπτική πτύχωση έχει επίδραση και στην επίπεδη διασύνδεση, μεταξύ υλικών διαφορετικού ιξώδους. Όταν συμβαίνει αυτό οι πτυχές παρουσιάζουν μια χαρακτηριστική σχηματοποίηση: κλίνουν προς την ίδια κατεύθυνση έχοντας ένα ευρύ στρογγυλεμένο σχήμα, λοβοειδείς (lobate) πτυχές, των οποίων οι αρθρώσεις τους, κλίνουν προς την αντίθετη κατεύθυνση, έχοντας ένα στενό  ή αιχμηρό (cuspate) σχήμα, και δείχνουν πάντα προς το υλικό με το μεγαλύτερο ιξώδες.

Έτσι, αν ένας σχηματισμός χαρακτηρίζεται από αιχμηρές-λοβοειδείς πτυχές (cuspate-lobate folds) μπορούμε να διακρίνουμε ποιά στρώματα ήταν σχετικά σκληρότερα συγκρινόμενα με τις παρακείμενες στρώσεις κατά τη διάρκεια της πτύχωσης. Αυτό είναι συνηθισμένη αίτια των mullion δομών.

Οι mullion δομές σχηματίζονται σε χονδροειδή γράμμωση και σε πετρώματα που έχουν υποστεί μεγάλη παραμόρφωση. Σχηματικά είναι μακριές κυλινδρικές δομές των οποίων η επιφάνεια μπορεί να είναι στρογγυλεμένη ή ανώμαλη όπως ένα ρυτιδωμένο φύλλο σιδήρου. Εσωτερικά, τα πετρώματα από τα οποία οι mullion απαρτίζονται είναι σκληρά και συμπαγή.

Κινηματικά μοντέλα πτύχωσης: κάμψεις ολίσθησης, ροής και ορθογώνιες

(Flexural-slip, flexural-flow and orthogonal flexure). - Πτυχές Τάξης 1Β

Μια πολυστρωμάτωση μπορεί να είναι ένας σωρός ανθεκτικών στρωμάτων διαχωριζόμενος από επιφάνειες ασυνέχειας ή από εναλλασσόμενα στρώματα με μεγάλες διακυμάνσεις ανθεκτικότητας (ανισότροπα). Οι μηχανικές συνέπειες είναι ότι τα ανθεκτικά στρώματα, σε κάθε πλευρά της ασυνέχειας η του αδύναμου στρώματος, μπορούν εύκολα να ολισθήσουν μεταξύ τους. Αυτή η διάτμηση “αποσυνδέει” τα στρώματα επιτρέποντας μια πτυχή να αναπτύξει μεγαλύτερη κάμψη ώστε η σωρός να μην παραμορφώνεται ως ένα ενιαίο στρώμα.

 Η καμπτική ολίσθηση (flexural-slip) περιγράφει μία διακριτή ρωγμάτωση η οποία συνήθως συμπίπτει με κυρτωμένες επιφάνειες και με πτυχώσεις. Το πάχος κάθε στρώματος δεν μεταβάλλεται και ως εκ τούτου σχηματίζουν παράλληλες πτυχές. Η ολίσθηση είναι ένας σημαντικός παράγων της πτύχωσης διότι οι τάσεις των παράλληλων στρωμάτων αυξάνονται με την αύξηση της περιστροφής των σκελών.

Όταν η διατμητική τάση υπερβαίνει την αντίσταση των αδύναμων στρωμάτων ή των στρωμάτων των περιθωρίων, τα δυνατότερα στρώματα των σκελών ολισθαίνουν το ένα πάνω στο άλλο προς τη κατεύθυνση και (συνήθως) κάθετα των αρθρώσεων, οι οποίες είναι σταθερές από στρώμα σε στρώμα. Επομένως οι γραμμές λείανσης (slickenlines) και η ανάπτυξη των ινωδών ορυκτών ή άλλοι δείκτες μετακινήσεων, δείχνουν ανάστροφη κατά κλίση ολίσθηση (dip-slip) στα κυρτωμένα επίπεδα εντός των σκελών των πτυχών, το οποίο αποτελεί κοινό κριτήριο για την καμπτική ολίσθηση.

Οι τιμές ολίσθησης είναι μεγαλύτερες στα σημεία κλίσης των σκελών και μειώνονται στο μηδέν στο άξονα άρθρωσης. H εκτόπιση (displacement) αυξάνεται καθώς η πτυχή σφίγγει και η οποία, επιπλέον, εξαρτάται από την απόσταση μεταξύ των ολισθαινόντων επιπέδων.

Σημειώστε ότι η ολίσθηση στη ζώνη άρθρωσης συνεπάγεται κινήσεις αντίθετης διεύθυνσης από το ένα σκέλος στο επόμενο, καθώς επίσης η συνοχή διατηρείται από το αντίκλινο στο σύγκλινο. Η θερμοκρασία και η πίεση στις οποίες ξεκινά η πτύχωση καμπτικής ολίσθησης είναι γενικώς χαμηλές.

Η καμπτική ροή (flexural-flow) περιγράφει παράλληλη διατμητική κάμψη, ομοιογενώς κατανεμημένη εντός όλκιμου στρώματος, το οποίο πτυχώνεται, μεταξύ σκληρών στρωμάτων. Όπως και στην καμπτική ολίσθηση, η παράλληλη διατμητική κάμψη στα σκέλη αναπτύσσεται αντίθετα κατά μήκος του αξονικού επιπέδου. Η παραμόρφωση που οφείλεται στη διάτμηση στη ζώνη άρθρωσης, τείνει να αναπτύσσει παχύτερες αρθρώσεις μεταξύ λεπτότερων σκελών, όπως οι ροϊκο-καμπτικές πτυχές (flexural – flow faults). Μερικές φορές η καμπτική ροή εφαρμόζεται σε αδύναμα στρώματα όπου έτσι ενεργοποιεί την κίνηση της παράλληλης στρωμάτωσης εντός μεγαλύτερων παράλληλων πτυχών, σε περιβάλλον χαμηλού βαθμού μεταμόρφωσης.

Σ΄ αυτή τη περίπτωση, τα ανθεκτικά στρώματα τείνουν να διατηρούν το πάχος τους καθ’ όλη τη διαδικασία της παραμόρφωσης, καθώς επίσης διαμορφώνουν το συνολικό σχήμα των συγκεντρικών και/ή παράλληλων πτυχών, ενώ τα μη ανθεκτικά στρώματα υπόκεινται σε καμπτική ροή.

Προκειμένου να διατηρηθεί η ομοιότητα, από στρωμάτωση σε στρωμάτωση, εύπλαστα υλικά μετακινούνται από τα σκέλη στις αρθρώσεις. Σε φυσικά παραδείγματα τέτοιων όμοιων πτυχών διακρίνεται έντονη φύλλωση στα σκέλη τους, η οποία “σβήνει” καθώς κινείται προς τις ζώνες αρθρώσεις.

H ορθογώνια κάμψη (orthogonal flexure) είναι ένας τύπος παραμόρφωσης με συγκεκριμένες προϋποθέσεις: όλες οι γραμμές που ήταν αρχικά ορθογώνιες με την στρωμάτωση παραμένουν έτσι καθ΄ όλη τη διάρκεια της παραμόρφωσης, ούτως ώστε το εξωτερικό μέρος εκτείνεται και το εσωτερικό του πτυχόμενου σώματος βραχύνεται καθώς επίσης μια ουδέτερη (neutral) επιφάνεια (χωρίς παραμόρφωση) διαχωρίζει το εξωτερικό από το εσωτερικό περιθώριο. Να σημειωθεί ότι τέτοια ουδέτερη επιφάνεια δεν υπάρχει στην καμπτική ροή. Ακόμη σχηματίζονται παράλληλες πτυχές συνήθως σε σκληρά στρώματα που αντιστέκονται σε όλκιμη (πλαστική) παραμόρφωση.

Το μοντέλο αυτό ονομάζεται και εφαπτομενική διαμήκης παραμόρφωση (tangential longitudinal strain), καθώς η στρεβλωτική παραμόρφωση είναι εσωτερική και συγκεντρώνεται στη ζώνη άρθρωσης αφήνοντας τα σκέλη σχετικά απαραμόρφωτα.

Επίδραση της ανισοτροπίας

Η καπτόμενη παράλληλη ανισοτροπία είναι μια εγγενής ιδιότητα της πολυστρωμάτωσης. Θεωρητικές και πειραματικές μελέτες, σε ομοιογενείς ανισότροπες πολυστρωματώσεις, έδειξαν ότι υπάρχει ένα εύρος σχημάτων πτυχών, οι οποίες μπορούν και σχηματίζονται κάτω από ανισότροπη παράλληλη συμπίεση η οποία και προσδιορίζει τον τύπο της πτυχής. Σε πολυστρωμάτωση με ασθενή ανισοτροπία συμμετρικές και ημιτονοειδείς πτυχές, μεταβάλλονται καθώς αυξάνει η ανισοτροπία σε πτυχές με ελαφρώς αποκλίνοντα αξονικά επίπεδα οι οποίες και επικρατούν σε πολυστρωμάτωση υψηλής ανισοτροπίας. Τα σχήματα των πτυχών διαδίδονται, από το πτυχώμενο στρώμα, σε μεγαλύτερη απόσταση σε ένα ανισότροπο παρά σε ισότροπο σώμα. 

Πτύχωση ροής (Flow folding).

Η πτύχωση ροής αναφέρεται στον σχηματισμό παθητικών πτυχών από ετερογενή διάτμηση ή ροή μηχανικών ισότροπων πετρωμάτων. Παραδείγματα είναι οι πτυχές που σχηματίζονται από μεταβολές του ποσού της ροής κατά την διάρκεια της απόθεσης πυριγενών σωμάτων με μαγματική υφή. Η πτύχωση ροής επίσης παρατηρείται σε εκροές λάβες, σε αργή ροή άλατος, πάγου και σε κορεσμένο νερό μη ενοποιημένων ιζημάτων.

Θεωρητικά, πτυχές ροής μπορούν να σχηματισθούν τόσο από ετερογενή απλή διάτμηση όσο και από καθαρή διάτμηση χωρίς αρχική διατάραξη των στρωμάτων. Τα στρώματα, με πολύ μικρή ανθεκτικότητα, συμπεριφέρονται πανομοιότυπα ως προς το υλικό που τα περιβάλλει με ομοιόμορφο ιξώδες. Όταν οι γραμμές ροής αποκλίνουν ή συγκλίνουν, το πάχος του στρώματος υπολογίζεται από τις αυξομειώσεις της ροής οι οποίες είναι αντιστρόφως ανάλογες ως προς τη κανονική απόσταση μεταξύ των γραμμών ροής. Συγχρόνως παρατηρείται επαναπτύχωση, η οποία είναι κοινό χαρακτηριστικό των ιξωδών και ασταθών ροών. Μια κλασσική σύγκριση είναι η κίνηση του λαδιού σε επιφάνεια νερού.

Να σημειωθεί ότι ροές πτυχής δεν σχηματίζονται από ολίσθηση κατά μήκος φύλλωσης καθώς αυτή δεν είναι μετακινούμενο επίπεδο.

Διατμητική πτύχωση (Shear folding)

Ως διατμητική πτύχωση θεωρούμε την πτύχωση που μπορεί να αναπτυχθεί εάν τα στρώματα βρίσκονται, αρχικά, σε συστολικό πεδίο ή όπου τα στρώματα περιστρέφονται στο εν λόγο πεδίο λόγω ανωμαλιών στην διατμητική ζώνη. Σε ζώνες υψηλής έντασης διατμητικής παραμόρφωσης η πτύχωση είναι συνεχής κατά την διάρκεια της διάτμησης. Οι παραγόμενες πτυχές μπορούν να θεωρηθούν ως παθητικές εάν η διαφορά ανθεκτικότητας μετάξι των στρωμάτων είναι αμελητέα κατά την διάρκεια της πτύχωσης. Αν η πτύχωσή είναι ενεργητική η παθητική αυτό θα φανεί από τη γεωμετρική ανάλυση, δεδομένου ότι οι παθητικές πτυχές είναι Τάξης 2 ενώ οι ενεργητικές είναι Τάξεων 2 & 3. Πτυχές σε ζώνες διάτμησης μπορούν να σχηματισθούν και διαφορετικά, όπως όταν η στρωμάτωση είναι κάθετη στα περιθώρια (τοιχία) της διατμητικής ζώνης, καθώς έτσι είναι η περίπτωση των απότομων διατμητικών ζωνών οριζόντιας ολίσθησης. Οι πτυχές, εδώ, σχηματίζονται με τις γραμμές άρθρωσης πλάγια στη ζώνη. Η λοξότητά τους εξαρτάται από τον αριθμό στροβιλότητας* (vorticity number) της ζώνης και από τον ακριβή προσανατολισμό της στρωμάτωσης σε σχέση με τη ζώνη διάτμησης.

*[ η στροβιλότητα δεικνύει πόσο γρήγορα περιστρέφονται τα σωματίδια σε μαλακό υλικό κατά την διάρκεια της παραμόρφωσης. Ο κινηματικός αριθμός στροβιλότητας (Wk) ισούται με 1 για την πλήρη διάτμηση και 0 για την καθαρή διάτμηση και οι ενδιάμεσες τιμές ισχύουν για την υποαπλή διάτμηση]

Λοξοζωνική γωνιώδης πτύχωση (Kinking – angular folding):

Πριν την παρακάτω περιγραφή πρέπει να τονίσουμε ότι η ένταση της πτύχωσης προσδιορίζει την διεύθυνση κατά την οποία τα σκέλη συγκλίνουν. Το σχήμα της πτύχωσης εξαρτάται από το πόσο η καμπυλότητα της πτυχωμένης επιφάνειας μεταβάλλεται γύρω από την άρθρωση, όπου μπορεί να είναι οξεία (μηδενική καμπυλότητα) ή να καμπυλώνει. Έτσι η ένταση της πτύχωσης περιγράφεται ως γωνιώδης ή στρογγυλεμένη αντίστοιχα. Οι οξύληκτες πτυχές έχουν αιχμηρή άρθρωση με, συνήθως, σιγμοειδή καμπτώμενα σκέλη.

Οι λοξοζωνικές (kink) πτυχές έχουν ευθεία σκέλη μεταξύ αιχμηρών και γωνιωδών αρθρώσεων των οποίων τα αξονικά επίπεδα καθορίζουν τα περιθώρια των λοξοζωνικών λωρίδων (kink band boundaries) που πιο απλά ονομάζονται λοξοζωνικά επίπεδα (kink planes). Τα κοντά σκέλη καθορίζουν τις λοξοζωνικές λωρίδες (kink bands).

Οι λοξοζωνικές (kink) λωρίδες αναπτύσσονται σε αυστηρά ανισότροπα πετρώματα όπου η ανισοτροπία αναγνωρίζεται είτε σε στρώματα περιορισμένου πάχους, είτε σε φύλλωση με πολύ λεπτές στρώσεις. Η χαρακτηριστική γεωμετρία τους οφείλεται σε γωνιακή περιστροφή λεπτών στρώσεων εντός των kink λωρίδων. Κανονικά, στην λοξοζωνική πτύχωση δεν παρατηρείται εσωτερική παραμόρφωση στις στρώσεις, αλλά μόνο περιστροφή γύρω από γωνία α των λοξοζωνικών αρθρώσεων. Επομένως η καμπτική ολίσθηση στα σκέλη συνδέεται εγγενώς με την λοξοζωνική πτύχωση ώστε να εξασφαλισθεί η συνέχεια των στρωμάτων διαμέσου των περιθωρίων των λοξοζωνικών λωρίδων.

Ο σχηματισμός kink λωρίδων ερμηνεύεται από τη θεωρητική ανάλυση της ιξώδους παραμόρφωσης των υλικών με μεγάλη επίπεδη ανισοτροπία. Αναπτύσσονται δύο μοντέλα βασικών μηχανισμών, τα οποία διαφέρουν ως προς τον τρόπο ανάπτυξης της λοξοζωνικής δομής και της γεωμετρίας της παραμόρφωσης, η οποία καθορίζεται από δύο γωνίες:

βi: μεταξύ του λοξοζωνικού επιπέδου και των εσωτερικών λοξοζωνικών στρωμάτων,

βe: μεταξύ του λοξοζωνικού επιπέδου και των στρωμάτων που βρίσκονται εκτός των kink λωρίδων.

Προκύπτουν δύο βασικοί μηχανισμοί:

1) Μετακινούμενα περιθώρια των λοξοζωνικών λωρίδων (ή κινούμενης άρθρωσης).

Τα δύο περιθώρια των λοξοζωνικών λωρίδων απομακρύνονται από μια κεντρική εμβρυακή γραμμή σε ένα μη παραμορφωμένο υλικό. Σ’ αυτή την περίπτωση οι γωνίες (βi, βe) παραμένουν σταθερές κατά την διεύρυνση των λοξοζωνικών λωρίδων.

2) Διατμητικές ζώνες λοξοζωνικών λωρίδων (ή σταθερής άρθρωσης)

Τα δύο περιθώρια των λοξοζωνικών λωρίδων ορίζουν τα σταθερά περιθώρια της ζώνης διάτμησης κατά το αρχικό στάδιο της ανάπτυξής των. Σ΄ αυτή την περίπτωση τα λοξοζωνικά τμήματα διατηρούν ένα σταθερό μήκος κατά την διάρκεια της προκαλούμενης διατμητικής περιστροφής. Αν βi>βe, η διαστολή λαμβάνει χώρα μεταξύ των λοξοζωνικών στρωμάτων. Περιστροφή μεγαλύτερη από βi=βe προκαλεί λέπτυνση των στρωμάτων, η οποία μπορεί να επιδράσει ως ανασταλτικός παράγων. 

Πειράματα αποκάλυψαν ότι οι kink λωρίδες συνήθως αναπτύσσονται σε συζυγείς ομάδες με αντίθετη ασσυμετρία όταν η μέγιστη συμπιεστική τάση είναι (υπο-) παράλληλος  ως προς ένα επίπεδο με προϋπάρχουσα ανισοτροπία.

Πάντως δεν αναπτύσσονται κατά μήκος επιπέδων υψηλής διατμητικής παραμόρφωσης, η οποία δείχνει ότι δεν είναι πραγματικές ζώνες διάτμησης. Ακόμη, κατ’ αναλογία με τα ρήγματα η φαινομενική και η σχετική μετατόπιση των στρωμάτων με επιμήκη σκέλοι δια μέσου των kink λωρίδων καθορίζει τρία είδη:

- Κανονικές kink λωρίδες όπου σημειώνεται βράχυνση.

- Αναστροφές kink λωρίδες όπου σημειώνεται επιμήκυνση.

- Ουδέτερες kink λωρίδες οι οποίες παραμένουν σταθερές.

Οξύληκτές γωνιώδεις πτυχές (Chevron folds).

Οι οξύληκτες γωνιώδεις πτυχές ομοιάζουν με τις λοξοζωνικές λωρίδες ως προς τα ευθέα σκέλη και ως προς το σχηματισμό κανονικών επίπεδων πολυστρωμάτων, αλλά οι ζώνες άρθρωσης δεν είναι γωνιακά κυρτωμένες. Η απαιτούμενη στρέβλωση (περιστροφή) εντοπίζεται στην άρθρωση ενώ αναπτύσσεται μια τυπική κάμψη ολίσθησης, καθώς τα επιμέρους στρώματα των σκελών δεν αντιμετωπίζουν εσωτερική στρέβλωση. Επειδή η μικρή άρθρωση σφίγγει μεταξύ των ευθείων σκελών, δημιουργούνται προβλήματα χώρου όπου ανοίγονται οπές μεταξύ των ανθεκτικών στρωμάτων. Ροή μεταξύ των αδύναμων ενδοστρώσεων, αν υπάρχει, γεμίζει αυτά τα κενά. Σε πολυστρωματώσεις με εναλλαγή ανθεκτικών και μη ανθεκτικών στρωμάτων, συνδυάζονται γεωμετρίες αυτών των πτυχών τόσο παράλληλες (σε ανθεκτικά) οστό κα όμοιες (σε μη ανθεκτικά). 

(Οι γωνιώδεις πτυχές της εικόνας αναφέρονται καί ως «γαλονοειδείς», προφανώς από το chevron που σημαίνει στρατιωτικά γαλόνια.)

Οι τύποι των πτυχών στα πετρώματα.
Πρέπει να σημειωθεί (και για λόγους σύγκρισης), ότι όπως έχει ήδη παρατηρηθεί, επιπρόσθετα από την κάμψη, υπάρχουν αρκετές διαδικασίες οι οποίες μπορούν να προκαλέσουν πτύχωση σε μια επιφάνεια.

Στο παραπάνω σχήμα [After Hudec & Jackson (2007),diagram design courtesy of F. Richards] φαίνεται η ταξινόμηση των δομών πτύχωσης, οι οποίες εξαρτώνται από το αν σχηματίζονται από επέκταση ή βράχυνση παράλληλων στρωμάτων και κάτω από εύθραυστες ή εύπλαστες συνθήκες:

a) Επίπεδο κανονικό ρήγμα το οποίο είναι πιθανό να παράγει παρελκτικές πτυχές.

b) Λιστρικό κανονικό ρήγμα με κυλινδρική πτύχωση.

c) Πτυχές καπτόμενου ρήγματος.

d) Επίπεδο ανάστροφο ρήγμα το οποίο είναι πιθανό να παράγει παρελκτικές πτυχές.

e) Κανονικό ρήγμα και εξαναγκαστική πτυχή με τρισδιατμητική ζώνη.

f). Μεταβατική ράμπα (μονόκλωνης κάμψης) μεταξύ των απολήξεων δύο κανονικών ρηγμάτων.

g) Ανάστροφο ρήγμα και εξαναγκαστική πτυχή με τρισδιατμητική ζώνη.

h) Πτυχή αποκόλλησης.

i) Επωθήσεις αντίκλινου.

j) Πτυχές διάδοσης ρήγματος.

k) Κανονική λοξοζωνική πτύχωση.

l) Συζυγείς αντίστροφες λοξοζωνικές πτυχές.

m) Καμπτικές πτυχές απλού στρώματος.

n) Καμπτικές πτυχές πολυστρωμάτωσης.

o) Εύθραυστή διείσδυση (διαπειρισμός) από δομό άλατος.

p). Εύπλαστη διείσδυση (διαπειρισμός από δομό άλατος.

Ζώνη απωθητικών πτυχών χαρακτηρίζουν το περιβάλλον όπου οι πτυχές αποκόλλησης (h), καπτόμενου ρήγματος (c) και διάδοσης ρήγματος (j) συνεπάγονται βράχυνση παράλληλων στρωμάτων  καθώς επίσης και εύθραυστης και εύπλαστης παραμόρφωσης.

Ο λόγος αμβλύτητας (Β) (bluntness ratio) είναι ποσοτική μέτρηση της βαθμού καμπυλότητας της άρθρωσης, δηλαδή πόσο καμπύλη ή οξεία είναι η άρθρωση. Καθορίζεται από τον λόγο των ακτινών: r_{h (}η ακτίνα της καμπυλότητας στην άρθρωση), ως προς r_i (η ακτίνα του κύκλου που εφάπτεται των σκελών στα σημεία κλίσης).

Να υπενθυμίσουμε  ότι, όταν το μήκος του αντίκλινου (που ο πυρήνας του περιέχει τα παλαιότερης ηλικίας πετρώματα) ή του σύγκλινου (που ο πυρήνας του περιέχει τα νεώτερης ηλικίας πετρώματα), είναι μικρότερο από το διπλάσιο του εύρους του, τότε ονομάζονται αντίστοιχα θόλος και λεκάνη.

Επαναπτυχώσεις 3D

Γωνιακές σχέσεις επαναπτύχωσης

Τύποι συμβολής δύο πτυχώσεων

Τύπος0 (σχήμα 2):αντιμετωπίζεται ως ειδική περίπτωση αφού η κορυφογραμμή και το ΑΕ είναι παράλληλα, πρόκειται για επαναπτύχωση δύο ταυτόσημων πτυχών.

Για την παρακάτω ανάλυση οι «τύποι» απεικονίζονται στα σχήματα 2 και 3 καθώς και οι γωνίες α,β,γ,δ στο σχήμα 1

Τύπος 1 (α=β=90⁰, γ=0⁰). Το αρχικό ΑΕ παραμένει επίπεδο, αλλά οι άξονες της υπερκείμενης πτυχής παραμορφώνονται. Αυτό προκαλεί ένα ισχυρό κυματισμό των κυρτώσεων της αρχικής πτυχής με αποτέλεσμα τον σχηματισμό θόλων και λεκανών όπου κάθε λεκάνη περιστοιχίζεται από 4 θόλους και κάθε θόλος από 4 λεκάνες όπως μία χαρτοαυγοθήκη (Thiessen, 1986). Αν α<90⁰ οι θόλοι και οι λεκάνες διευθετούνται σε en echelon (λοξή- κλιμακωτή) διάταξη (O'Driscoll, 1962).

Τύπος 2 (α=90⁰, β=γ=0⁰). Το αρχικό ΑΕ και ο αρχικός άξονας είναι παραμορφωμένοι. Αν η επαναπτυχωμένη δομή γίνεται προοδευτικά κάθετη στο b2 θα παρεμβάλλονται σχηματισμοί κυκλικής μορφής, στρογγυλεμένων τριγώνων, μορφής μανιταριού (Ramsay and Huber, 1987). Πάντως, πλάγια τμήματα, κυρίως αν οι επαναπτυχώμενες δομές αποκλίνουν από τον προσανατολισμό της τελικής επαναπτύχωσης, θα σχηματίζουν μια μεγάλη ποικιλία συνθέτων μορφών (Thiessen, 1986).

Τύπος 3 (α=β=0⁰, γ=90⁰). Το αρχικό ΑΕ είναι παραμορφωμένο αλλά οι αρχικοί άξονες δεν κάπτονται από την υπερκείμενη πτυχή. Παράλληλές εγκάρσιες τομές με τους άξονες b1 και b2 δεν θα αναπτύξουν περίπλοκους σχηματισμούς αλλά θα φαίνονται ως παράλληλες ευθείες γραμμές. Πάντως εγκάρσια στους άξονες πτυχών, θα φανούν παρεμβαλόμενοι σχηματισμοί συγκλίνοντες – αποκλίνοντες ή σχήματος άγκιστρου  (Thiessen, 1986).

Ο Τύπος 0 επαναπτυχωμένης δομής, σχηματίζεται πάντοτε όταν β=γ=90°. Στις δύο διαστάσεις η σχηματιζόμενη επαναπτύχωση δεν αναπτύσσει κάποιο παρεμβαλλόμενο σχηματισμό. Αν και οι Thiessen and Means (1980), παρατήρησαν δύο διαφορετικές γεωμετρικές περιπτώσεις επαναπτύχωσης του Τύπου 0, αλλά  θεωρήθηκαν ότι είναι δύσκολο να εντοπιστούν στη φύση.  Παρόλα αυτά. αν η αρχική πτύχωση διατμηθεί από μία φλέβα ή dyke με μεγάλη γωνία ως προς τον άξονα b1, οι μετασχηματισμοί είναι προφανείς και μπορούμε να ξεχωρίσουμε τρεις κατηγορίες, όπου απαιτείται και η χρήση της γωνίας δ (μεταξύ c1και c2):

Τύπος 01 (α=β=γ=δ=90⁰). Η διατμητική διεύθυνση της υπερκείμενης πτυχής είναι παράλληλη στον b1 αλλά τα ΑΕ c1 και c2 είναι κάθετα μεταξύ των. Η προκύπτουσα επαναπτύχωση είναι ταυτόσημη ως προς το σχήμα της αρχικής, αλλά δείχνει σαφώς την υπέρθεση μίας ετερογενούς παραμόρφωσης παράλληλα με τον οριζόντιο b2.

Τύπος 02 (α=β=γ=90⁰ , δ=0⁰). Η διατμητική διεύθυνση της υπερκείμενης πτυχής είναι παράλληλη στον b1 αλλά τα ΑΕ, c1 και c2 είναι παράλληλα μεταξύ των. Η προκύπτουσα επαναπτύχωση είναι ξανά ταυτόσημη ως προς το σχήμα της αρχικής και δείχνει σαφώς την υπέρθεση μίας ετερογενούς παραμόρφωσης παράλληλα με τον κάθετο b2.

Τύπος 03 (β=γ=90⁰ , α=δ=0⁰). Τα ΑΕ και οι άξονες της αρχικής και της υπερκείμενη πτυχής είναι παράλληλα μεταξύ των. Η προκύπτουσα δομής της επαναπτύχωσης δεν είναι ταυτόσημη στο σχήμα με τη αρχική, αν και αποτελεί μια παραλλαγή του Τύπου 0.

Στερεογράφημα (κινούμενο) επαναπτυχώσεων με σταθερό προσανατολισμό Δύση-Ανατολή του άξονα της αρχικής πτυχής και το κάθετο αξονικό επίπεδο με κατεύθυνση Βορά-Νότο.

Οι άξονες c2 των επαναπτυχώμενων Τύπων 02 και 03 έχουν προσανατολισμό Β-Ν, των Τύπων 1 και 2 έχουν Δ-Α και στο κέντρο τοποθετούνται οι Τύποι 3 και 01.

Οι επαναπτυχώμενοι Τύποι 1 -3 μπορούν να μετασχηματιστούν στους αντίστοιχούς τους 01-03 με την περιστροφή του αξονικού τους πεδίου γύρω από τον υπερκείμενο άξονα b2. Αυτός ο μετασχηματισμός μεταξύ των επαναπτυχώμενων Τύπων μπορεί να αποτυπωθεί από τα ίχνη του c2 είτε  κατά την περιστροφή είτε κατά μήκος των διαμέτρων Β-Ν και Δ-Α:

1. Ο Τύπος 1 τοποθετείται στην περιφέρεια με τον άξονά του στο Β και Ν και ο c2: Α και Δ. Μετασχηματίζεται στον Τύπο 01 με την μετακίνηση του c2 κατά μήκος της διαμέτρου Δ-Α και προς το κέντρο.

2. Ο Τύπος 2  τοποθετείται με τον άξονά του στο κέντρο και ο c2 στην Α και Δ. Μετασχηματίζεται στον Τύπο 02 κινώντας τον c2 επί της περιφέρειας με προσανατολισμό Β-Ν.

3. Ο Τύπος 3 τοποθετείται με τον  άξονά του στην Α και Δ, και ο c2 στο κέντρο. Μετασχηματίζεται στον Τύπο 03 με την μετακίνηση του c2 κατά μήκος της διαμέτρου Β-Ν και προς την περιφέρεια.

Σημειώστε ότι οι δομές, ουσιαστικά, διαφοροποιούνται από τον προσανατολισμό του b2.

Τρισδιάστατη απεικόνιση επαναπτυχώσεων με άξονες τις γωνίες α, β, γ με τιμές από 0⁰ -90⁰

ΔΥΝΑΜΙΚΗ ΑΝΑΛΥΣΗ ΚΑΜΠΤΟΜΕΝΩΝ ΠΤΥΧΩΝ

(εξίσωση Biot-Ramberg, αριθμός Deborah )

Μία σύντομη περιγραφή της εξίσωσης Biot-Ramberg:

Ανεξάρτητα αλλά σχεδόν ταυτόχρονα οι Biot και Ramberg ανέπτυξαν την εξίσωση για το επικρατούν (dominant) μήκος κύματος πτυχής.

Ο Maurice Biot μετά από την παρότρυνση του K. Hubbert (Shell Research and Development in Houston), δημοσίευσε το 1957, σε εργασία του για την γεωλογική θεωρία της πτύχωσης, την εξίσωση: L_d/T = 2 π (6μ/μ_ο)^1/3    όπου:

L_d= επικρατούν μήκος κύματος,

T= το πάχος του στρώματος,

μ= συντελεστής ιξώδους σκληρού υλικού (πτυχής) και

μ_ο = συντελεστής ιξώδους μαλακού υλικού (που ενσωματώνει την πτυχή).

Δηλαδή το μήκος κύματος πτυχής είναι ευθέως ανάλογο ως προς το πάχος του στρώματος (που αναπτύσσεται η πτυχή) και ως προς την κυβική ρίζα του λόγου ιξώδους των δύο υλικών.

Παράλληλα, ο Hans Ramberg στην Uppsala (Σουηδία), είχε ξεκινήσει την ανάλυση της πτύχωσης ενός στρώματος ενσωματωμένο σε ένα σώμα μικρότερου ιξώδους. Το 1959 παρουσίασε την ίδια εξίσωση του Biot, με την διαφορά ότι αντί για «6» είχε βάλει μια απροσδιόριστη σταθερά διότι δεν ήταν σίγουρος πώς να αξιολογήσει την επίδραση του λόγου των ιξωδών. Τελικά το 1961 απέδειξε ότι η εξίσωση του Biot (με το «6») ήταν η καλύτερη προσέγγιση για τη λύση του προβλήματός του.

Θεωρία

Αξιοσημείωτο πλήθος εργασιών απέδειξαν, θεωρητικά και πειραματικά, ότι αν ένα λεπτό στρώμα υποβάλλεται σε παράλληλη βράχυνση και είναι περισσότερο συνεκτικό (πχ σκληρότερο) από το περιβάλλοντα αυτό υλικό, αυτή η κατάσταση χαρακτηρίζεται ασταθής διότι κάποιες αρχικές γεωμετρικές διαταραχές στο σκληρό στρώμα θα δημιουργήσουν διεύρυνση και κάμψη ενώ ολόκληρο το σύστημα (το στρώμα με το περιβάλλον υλικό) παραμορφώνεται με καθαρή διάτμηση.

Οι αρχικές εργασίες επικεντρώθηκαν στην ανάλυση της κάμψης και διαχειρίστηκαν το πρόβλημα με την παραδοχή ότι όλα τα στρώματα έχουν ελαστική συμπεριφορά. Η προϋπόθεση της γραμμικής σχέσης μεταξύ τάσης και παραμόρφωσης και των λόγων αυτών έκαναν, απλά, το όλο πρόβλημα εύκολο στον χειρισμό.

Σ΄ αυτά που ακολουθούν έχουν γίνει οι παρακάτω βασικές υποθέσεις:

1) Οι πτυχές θεωρούνται μικρές ώστε η βαρύτητα να μην αποτελεί σημαντικό παράγοντα στην ανάπτυξή τους.

2) Η συμπίεση είναι παράλληλη με το στρώμα.

3) Η παραμόρφωση είναι επίπεδη.

Η κάμψη δημιουργεί ένα σύστημα πτύχωσης που έχει συμμετρικό, περιοδικό, ημιτονοειδές σχήμα. Η ανάλυση ξεκινά με την πυρηνοποίηση, δηλαδή από τη πτυχή κάμψης που προκύπτει μετά από απειροελάχιστη παραμόρφωση.

Από μαθηματική άποψη αν ένα «τέλειο» σώμα συμπιέζεται πλαγίως, τότε απλώς, κατά τη διάρκεια της βράχυνσης, θα λεπτύνει χωρίς να πτυχωθεί. Απαιτείται μία ατέλεια για να επιφέρει καμπτική πτύχωση. Αυτή η αρχική ατέλεια μπορεί να προϋπάρχει στο στρώμα προτού εφαρμοστεί η συμπίεση ή μπορεί να υπάρχει μια τοπική αστάθεια που αναπτύσσεται καθώς εφαρμόζεται η συμπίεση.

Τεχνικά, η πτύχωση προσομοιώνεται με μία ή περισσότερες αλλεπάλληλες μικρού εύρους ημιτονοειδείς συναρτήσεις, όπου περιγράφουν τα περιθώρια του στρώματος. Θεωρητικά γίνεται η υπόθεση ότι το μέσο που οριοθετεί το στρώμα προβάλει αντίσταση σε κάθετη εκτροπή του. Τότε το πλέον σταθερό σχήμα είναι αυτό που χρειάζεται τη λιγότερη άσκηση τάσης παράλληλα στο στρώμα, δηλ. τη λιγότερη ενέργεια ελαστικής παραμόρφωσης που εφαρμόζεται συγχρόνως στο στρώμα και στο υλικό που το περιβάλλει. Αποτελέσματα ερευνών έδειξαν ότι, αν και όλες οι πρωταρχικές διαταραχές μπορεί να αρχίσουν να διαμορφώνονται για την εκκίνηση πτύχωσης, μόνο μία ημιτονοειδής απόκριση αναπτύσσεται σε πτύχωση με ένα συγκεκριμένο μήκος κύματος καθώς η παραμόρφωση εξελίσσεται. Αυτό είναι το επικρατούν μήκος κύματος.

Επικρατούν μήκος κύματος.

Τα βασικά μεγέθη που προσδιορίζουν το επικρατούν μήκος κύματος είναι:

- το πάχος του στρώματος και

- ο λόγος ιξώδους (διαφορά στερεότητας) μεταξύ στρώματος και σώματος, τα οποία και τα δύο θεωρούνται ως Νευτώνεια ιξώδη υλικά. 

Για ένα στρώμα συγκεκριμένους πάχους (h) και ιξώδους (μ_L) το οποίο ενσωματώνεται σε ένα σώμα (matrix) απροσδιόριστου πάχους και μικρότερου ιξώδους (μ_M), αναπτύσσονται  εσωτερικές δυνάμεις (Fint) ως η αντίσταση του συγκεκριμένου στρώματος καθώς επίσης και εξωτερικές δυνάμεις (Fext) ως η αντίσταση του σώματος, τότε το επικρατούν μήκος κύματος (W_d) είναι αυτό με τη μικρότερη συνολική δύναμη (Ftot=Fint+Fext) και το οποίο περιγράφει η εξίσωση Biot-Ramberg:

 W_d=2πh(μ_L/6μ_M)^1/3        (1)

Αυτή η εξίσωση έχει επαληθευθεί πειραματικά και αριθμητικά και μπορεί να εφαρμοστεί μόνο σε μικρού πλάτους πτυχές, η οποία υποδηλώνει ότι:

1)Το μήκος κύματος είναι ανεξάρτητο και της τιμής του συμπιεσμένου βάρους και του βαθμού της παραμόρφωσης.

2) Το μήκος κύματος είναι ευθέως ανάλογο ως προς το πάχος του στρώματος, έτσι ώστε, διαφορετικά μήκη κυμάτων εμφανίζονται σε διαφορετικά στρωμάτων ποικίλης παχύτητας, όπου σε όλα η παραμόρφωση βράχυνσης είναι σταθερή. Παχύτερα στρώματα παράγουν μακρύτερα μήκη κυμάτων. Διαφορετικές εντάσεις ανάπτυξης πτυχών δεν υποδεικνύουν και διαφορετικές εντάσεις παραμόρφωσης του h.

3) Το μήκος κύματος εξαρτάται μόνο από τη κυβική ρίζα του λόγου ιξωδών στρώματος – σώματος.

Η επίδραση του λόγου αντοχής (strength) ως προς το λόγο μήκος κύματος/βαθμού πάχους, φαίνεται γράφοντας τη (1) ως:

 W_d/h=2π(μ_L/6μ_M)^1/3                       (2)

Αν λύσουμε την (2) ως προς το λόγο των ιξωδών: μ_L/μ_M=0,02419 (W_d/h)³        (3)

Στην περίπτωση που τα ιξώδη τείνουν να ισορροπούνε δηλ. ο λόγος μ_L/μ_M τείνει στην μονάδα, τότε το επικρατούν μήκος κύματος (W_d) τείνει στην τιμή 3,4577 h (περίπου 3,5 φορές το πάχος).

Στο σημείο αυτό πρέπει να επισημανθεί ότι η ανάλυση των παραμέτρων του επικρατούντος μήκους κύματος προσδιορίζεται και με την εφαρμογή της ρεολογίας (επιγραμματικά):

α) Νόμος του Νεύτωνα του ιξώδους: τ = n γ

τ= διατμητική τάση, n=συντελεστής ιξώδους, γ= ρυθμός διάτμησης

αν n=1: νευτώνεια υλικά,  0<n<1: το ιξώδες μειώνεται με το ρυθμό διάτμησης, n>1 το ιξώδες αυξάνεται με το ρυθμό διάτμησης.

β) Νόμος του Oswald-de Waele (Νόμπελ Χημείας 1909): τ = mγⁿ

m= δείκτης συνοχής, (όσο μεγαλύτερο το m τόσο πιο ιξώδες το υλικό)

n= δείκτης ρεολογικής συμπεριφοράς που δείχνει το βαθμό μη Νευτώνειας συμπεριφοράς του υλικού (για 0<n<1, ή n>1 και n ≠1).

Ρυθμός ανάπτυξης

Ο ρυθμός ανάπτυξης μίας πτυχής προσδιορίζει τον ρυθμό της διεύρυνσής της (amplification*). Ως εκ τούτου, η ερώτηση είναι, πόσο γρήγορα τα σημεία άρθρωσης κινούνται, κατά την διαδικασία της κάμψης, προς τα πάνω ορθογωνίως στη κατεύθυνση του αντίκλινου ή και αντίθετα τα πυθμιαία προς το σύγκλινο; Εξ ορισμού το επικρατούν μήκος κύματος είναι εκείνο το οποίο διευρύνεται στον ταχύτερο ρυθμό ανάπτυξης. Άρα από την εξίσωση (1) το πάχος του καπτόμενου στρώματος και το ιξώδες του ως προς το ιξώδες του περιέχοντος αυτό σώματος, είναι οι παράμετροι οι οποίοι προσδιορίζουν τον βαθμό διεύρυνσης. Ο ρυθμός ανάπτυξης αυξάνεται ευθέως ανάλογα με την διαφορά ιξώδους μεταξύ στρώματος και σώματος.

 *amplification: για την περίπτωση της ανάπτυξης των πτυχών, ο όρος δεικνύει την αύξηση του εύρους των και θα αποδοθεί ως «διεύρυνση».

Η διεύρυνση είναι το άθροισμα δύο παραμέτρων: της κινηματικής και της δυναμικής ανάπτυξης.

A_k: ο κινηματικός (παθητικός) ρυθμός ανάπτυξης που οφείλεται στο πάχος του σώματος.

A_d: ο δυναμικός ρυθμός ανάπτυξης που οφείλεται στην διεύρυνση της αρχικής μηχανικής αστάθειας.

Το εύρος Α μίας ιξώδους κάμψης συσχετίζεται εκθετικά με τον χρόνο (t) ως ακολούθως:

 A=A₀ e^Pat   όπου:

Α₀=το αρχικό εύρος της ημιτονοειδούς διαταραχής. Η παρουσία του στην παραπάνω εξίσωση συνεπάγεται ότι η διεύρυνση της αρχικής διαταραχής επηρεάζει την τελική γεωμετρία του μήκος κύματος.

P_A=είναι ο συντελεστής διεύρυνσης, (amplification factor) ο οποίος καθορίζει τον ρυθμό της διεύρυνσης και περιλαμβάνει το άθροισμα (A_k +A_d)_.

Επειδή η ανάπτυξη των πτυχών κάμψης είναι μία ασταθής διαδικασία θα διευκόλυνε, για την ανάλυσή της, ο διαχωρισμός της σε τέσσερα στάδια:

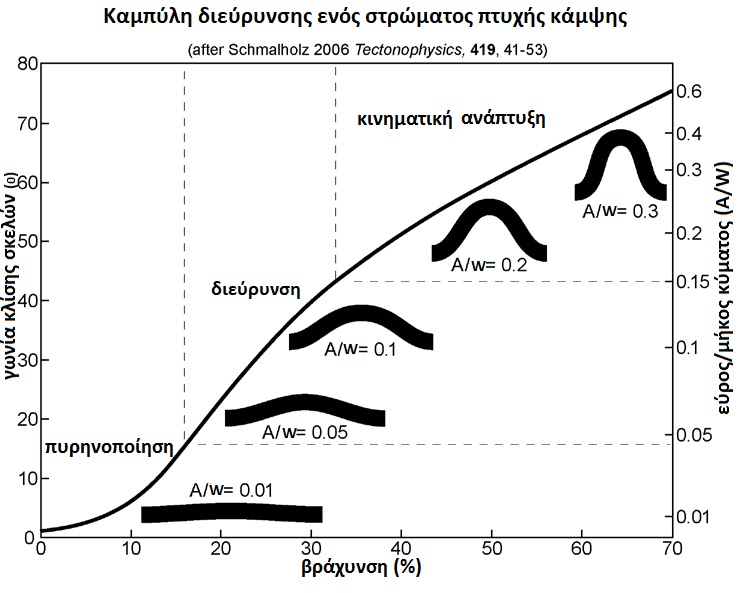
1) Επώαση (incubation): αρχική ομοιογενής βράχυνση.

Σε πειραματικές κάμψεις, τα συμπιεσμένα στρώματα δεν πτυχώνονται για το  πρώτο 20% περίπου της βράχυνσης. Αντ’ αυτού τα στρώματα αυξάνουν τόσο το πάχος τους, όσο απαιτείται για την αντιστάθμιση της παράλληλης προς αυτά βράχυνσης. Το ποσό της ομοιογενούς ελαστικής ή ανελαστικής παραμόρφωσης, πριν την εκκίνηση της κάμψης, είναι συνάρτηση του βαθμού της παραμόρφωσης και των σχετικών μηχανικών ιδιοτήτων των στρωμάτων που υφίστανται την κάμψη. Το πάχος των στρωμάτων παραμένει σταθερό και επομένως δεν υπάρχει διατμητική παραμόρφωση εντός και παράλληλα των προς βράχυνση στρωμάτων.

2) Πυρηνοποίηση (nucleation).

Η ενεργοποίηση της κάμψης είναι δύσκολη και γενικώς απαιτεί κάποια μορφή διαταραχής για την αρχική βράχυνση/πάχυνση του στρώματος. Η πυρηνοποίηση συνεπάγεται περιστροφή του στρώματος σε συγκεκριμένα σημεία όπου υπάρχουν εγγενής (πχ αρχική καμπτική μεταβολή) ή παραγόμενες (πχ τοπική διακύμανση της τάσης που ασκείται στο περιθώριο) ετερογένειες στην παραμόρφωση. Ένα συγκεκριμένο μήκος κύματος διαταραχής διευρύνεται επιλεκτικά. Αυτή η διεύρυνση σχηματίζει τις πτυχές κάμψεις καθώς το επιλεγμένο μήκος κύματος συσχετίζεται με τα μηχανικά χαρακτηριστικά των σκληρών στρωμάτων.

3) Διεύρυνση (amplification).

Διεύρυνση είναι η προοδευτική κάθετη ανάπτυξη της πτυχής. Θεωρητικές εργασίες σχετικές με την πτύχωση και την προκύπτουσα απ’ αυτή έννοια του επικρατούντος μήκος κύματος, ισχύουν μόνο για την για την αρχική εκκίνηση (πχ πυρηνοποίηση) της κάμψης όπου το εύρος της πτυχής είναι τόσο μικρό ώστε καθίσταται πρακτικά αόρατο. Μόλις ξεκινήσει η κάμψη, η βράχυνση θα μπορεί να συνεχιστεί με την περιστροφή των σκελών, έτσι ώστε η κάμψη να γίνεται, προοδευτικά ευκολότερη και η κλίση των σκελών να αυξάνεται ταχέως συγκρινόμενη με τον βαθμό βράχυνσης. Η κάμψη σ’ αυτό το στάδιο είναι μία διαθρωτική διαδικασία της μαλάκωσης, δηλ. η αντίσταση του στρώματος ως προς την βράχυνση, μειώνεται, με προοδευτική παραμόρφωση (διεύρυνση) ενώ οι ιδιότητες του υλικού δεν μεταβάλλονται.

Η καμπτική πτυχή διευρύνεται σε ένα βαθμό που εξαρτάται από την διαφορά ολκιμότητας μεταξύ των σκληρών και μαλακών στρωμάτων (γρηγορότερη διεύρυνση για μεγαλύτερη διαφορά ιξωδών). Μια γωνία κλίσης 15^ο των σκελών είναι περίπου το όριο του εύρους για το οποίο η ανάλυση του επικρατούντος μήκος κύματος, όπως  καθορίζεται από την εξίσωση Biot – Ramberg,  δεν λειτουργεί.

Τα αδύνατα στρώματα συνεχίζουν να βραχύνονται ομοιογενώς ενώ η πτυχή διευρύνεται. Η προοδευτική βράχυνση του συστήματος είναι αποτέλεσμα δυο διεργασιών: η μία συσχετίζεται απευθείας με την κύρτωση των στρωμάτων για να σχηματίσουν τη πτυχή, η άλλη απαρτίζεται από μία επιπρόσθετη παραμόρφωση σε κάθε σημείο με μια συνιστώσα βράχυνσης και μια συνιστώσα επιμήκυνσης ως προς τον άξονα της πτυχής

4) Κλείδωμα (locking-up).

Περαιτέρω βράχυνση συνεχίζεται τόσο από τη συρρίκνωση όσο και από την κάμψη. Η συρρίκνωση σφίγγει την αρχική καμπτική πτυχή καθώς τα σκέλη λεπτύνονται και η άρθρωση πυκνώνει (πάχυνση). Αντίστοιχα, για την προοδευτική ανάπτυξη των πτυχών απαιτούνται περισσότεροι του ενός μηχανισμοί. Όταν τα σκέλη γίνονται παράλληλά μεταξύ τους (πχ, ισοκλινής πτυχή), δεν μπορεί η βράχυνση να συνεχιστεί περαιτέρω από την περιστροφή των σκελών, δηλαδή η δυναμική διεύρυνση της πτύχωσης σταματά. Η τελική μορφή συντελείται όταν κάθε σημείο της στρωμάτωσης έχει περιστραφεί σε μια σχεδόν σταθερή θέση όπου η αντίσταση στην παραμόρφωση έχει αυξηθεί. Αυτό αναφέρεται ως «κλείδωμα». 

Πολυστρωμάτωση (Multilayer)

Για την περιγραφή της συμπεριφοράς μίας πολυστρωματικής αλληλουχίας, απαιτούνται πολύπλοκες μαθηματικές εκφράσεις, διότι πρέπει να περιλαμβάνουν όλες τις μεταβλητές, ιδιαίτερα την απόσταση και τον βαθμό συνεκτικότητας μεταξύ των στρωμάτων της ακολουθίας. Επομένως, πειραματικές παραμορφώσεις σε ανάλογα μοντέλα θεωρούνται απαραίτητες για την ταυτοποίηση μερικών από τους φυσικούς συντελεστές, οι οποίοι σχετίζονται άμεσα με το σχήμα των πτυχών. Αυτά τα μοντέλα, που αποτελούνται από στρώματα διαφορών πυκνοτήτων (πάχους) και μηχανικών χαρακτηριστικών, είναι σύνθετα συστήματα τα οποία παρουσιάζουν συγκεκριμένες συμπεριφορές:

Στο 2^ο στάδιο (πυρηνοποίηση) η αστάθεια της κάμψης είναι συνάρτηση του μηχανικού χαρακτήρα και της θέσης των πλέον πυκνών και δύσκαμπτων στρωμάτων της ακολουθίας.

Στο 3^ο στάδιο (διεύρυνση) ενώ τα πλέον δύσκαμπτα και παχιά στρώματα κάμπτονται ως απλές μονάδες, η πολυστρωματική ακολουθία, ως ολότητα, θα υποστεί πτύχωση κάμψης – ολίσθησης (flexural-slip). Ο βαθμός και η φύση ανάπτυξης μικροδομών σε σχετικά μαλακά στρώματα θα εξαρτηθούν από το τοπικό περιβάλλον της παραμόρφωσης το οποίο δημιουργείται κατά την διάρκεια της πτύχωσης των σκληρότερων στρωμάτων.

 Κατανομή τάσης (Stress distribution)

1. Στις ζώνες άρθρωσης, η μεγαλύτερη τάση συμπίεσης που ασκείται αν:

α) είναι παράλληλη ως προς το στρώμα των κοίλων πλευρών των πτυχών συντελεί στη βράχυνση του παράλληλου στρώματος και αν

β) είναι κάθετος (περίπου) στο στρώμα των κυρτών πλευρών συντελεί στην επιμήκυνση του παράλληλου στρώματος.

2. Στα σκέλη, η μεγαλύτερη τάση συμπίεσης που ασκείται τείνει να περιστραφεί μαζί με τα σκέλη έως ότου η κλίσης τους πλησιάσει στα όρια της (μηδενική γωνία), όπου σ’ αυτό το σημείο επανέρχεται στον αρχικό προσανατολισμό και τείνει να σχηματίσει την μεγαλύτερη γωνία της κύρτωσης.

Το μέγεθος της τάσης μεταβάλλεται εγκάρσια στην πτυχή και καθ’ όλη την διάρκεια της παραμόρφωσής της. Αυτές οι μεταβολές συντελούν ώστε, το στρώμα να μεταφέρει στο σύστημα  ένα μεγάλο ποσοστό της ασκούμενης δύναμης όταν είναι παράλληλο στη διεύθυνση της βράχυνσης, αλλά αυτή η διαδικασία ενίσχυσης μειώνεται καθώς τα σκέλη περιστρέφονται σε μεγαλύτερες γωνίες.

Επίδραση της διαφοράς του ιξώδους.

Καμπτικές πτυχές ενός στρώματος.

Αυτές οι πτυχές αναπτύσσονται σε μεγάλη ποικιλία σχημάτων διότι λόγω της εξάρτησης των ροών από την θερμοκρασία, σε μία αύξησή της μεταβάλλεται η μηχανική συμπεριφορά του συστήματος και επομένως επηρεάζει τη γεωμετρία των αναπτυσσόμενων πτυχών.

- Αν το ανθεκτικό στρώμα είναι πολύ σκληρότερο από το περιβάλλον σώμα, (μ_L/μ_M>50), τότε ο ρυθμός διεύρυνσης της κάμψης είναι πολύ γρήγορος και το σκληρό στρώμα εκτρέπεται δυναμικά προς υλικό χαμηλότερης ανθεκτικότητας. Πτυχές, με μεγάλο μήκος κύματος, συγκρινόμενες με το πάχος, του αρχικά ανεπτυγμένου ανθεκτικού στρώματος, προκύπτει ότι το μήκος του έχει υποστεί ελάχιστες έως μηδενικές αλλαγές. Κατά τη διάρκεια περαιτέρω παραμόρφωσης, τα σκέλη περιστρέφονται σε γωνίες μεγαλύτερες των 90⁰ και ως εκ τούτου παράγονται μεγάλα μήκη κύματος σε στρογγυλεμένους σχηματισμούς όπως οι πτυγματικές πτυχές.

- Αν η σχέση ιξωδών είναι χαμηλή (μ_L/μ_M<10) ο ρυθμός διεύρυνσης είναι αργός και δεν είναι πιθανός ο σχηματισμός πτύχωσης. Αντ’ αυτού η προκύπτουσα παραμόρφωση θα αποτελείται από στρώματα που έχουν υποστεί βράχυνση και μερική λέπτυνση, η οποία εκφράζεται, στα περιθώρια του ανθεκτικού στρώματος, με μικρή διεύρυνση και μικρά μήκη κύματος. Στην περίπτωση περαιτέρω βράχυνσης αυτές οι πτυχές θα παρουσιάζουν εναλλασσόμενα κυκλικά και αιχμηρά σχήματα και είναι οι αιχμηρές-λοβοειδείς όπως περιεγράφηκαν παραπάνω.

Το ερώτημα που τίθεται, είναι σε ποια τιμή η βράχυνση του αρχικού στρώματος θα επαληθεύει την εξίσωση του επικρατούντος μήκος κύματος των Biot- Ramberg.

Η Jo-Ann Sherwin και ο William Chapple (1968), βασιζόμενοι σε πραγματικές μετρήσεις (όχι εργαστηρίου) πτυχών απλών στρωμάτων, κυρίως σε χαλαζιακές φλέβες σε φυλλιτικά πετρώματα σχιστόλιθων και ψαμμιτών, βρήκαν ότι ο λόγος W_d/h ήταν στην πραγματικότητα χαμηλότερος καθώς και η συνολική καμπυλότητα του W_d επίσης σημαντικά χαμηλότερη απ’ αυτούς που είχε προβλέψει η θεωρία των Biot- Ramberg. Υποστήριξαν ότι ακόμη και με αυτό το μικρό ποσό ιξώδους υπάρχει μια σημαντικά υπολογίσιμη αστάθεια για την οποία η βράχυνση του στρώματος, κατά την διάρκεια της πτύχωσης είναι βέβαιο ότι δεν μπορεί πλέον να αγνοείται. Ως εκ τούτου τροποποίησαν την ανάλυση των Biot- Ramberg. λαμβάνοντας υπόψη το αποτέλεσμα της σημαντικότητας της βράχυνσης και του πάχους, τα οποία συνοδεύουν την πτύχωση και κατέληξαν στη παρακάτω σχέση για τον λόγο W_d/h (όπως ακριβώς την έγραψαν):

L_d/T=2π[μ/6μ₀((1+λ)/2λ²)]^1/3   και για άμεση σύγκριση παρατίθεται η εξίσωση των Biot- Ramberg: L_d/T = 2π(6μ/μ_ο )^1/3    :

Το λ το όρισαν ως η ομοειδής, πεπερασμένη επιμήκυνση η οποία διαμορφώθηκε κατά την ανάπτυξη της πτυχής.

Οι Sherwin and Chapple θεώρησαν ακόμη αναγκαίο να περιγράψουν την διάταση (stretch) ως δύο διατάσεις εντός του επιπέδου του στρώματος, παράλληλα και κάθετα προς την διεύθυνση βράχυνσης. Τελικά ο Hudleston (1973) επανέγραψε την εξίσωσή τους, με την παραπάνω παραδοχή, έτσι ώστε, όμως, να είναι συγκρίσιμη με των Biot Ramberg:

 W_d=2πh[(μ_L(S-1)/6μ_M 2s²]^1/3       (4)

 Όπου s² =λ₁/λ₃, και λ₁, λ₃ είναι οι κύριες τετραγωνικές μηκύνσεις κάθετα και παράλληλα αντίστοιχα στο στρώμα (σε συμφωνία με τους σ₁ και σ₃).

Προφανές γίνεται ότι, από την παραπάνω εξίσωση (4), ότι το επικρατούν μήκος κύματος αλλάζει με τη παραμόρφωση. Θεωρητικά προβλέπεται ότι καθώς η παραμόρφωση προχωρά οι πτυχές με προοδευτικά μεγαλύτερη αναλογία πάχους στρώματος προς μήκος κύματος θα είναι οι περισσότερο διευρυμένες. Καθώς το πάχος μεταβάλλεται, η έννοια του επικρατούντος μήκους κύματος θα πρέπει να προσαρμοσθεί στο νέο πάχος του στρώματος (h_n), για το οποίο ένα προτιμητέο μήκος κύματος (preferred wavelength) W_p υπολογίζεται (Biot,1965a, p. 427, and Johnson and Pfaff (1989):

 

 W_p / W_d = (h_n /h) S       (5)

Όπου S είναι η κύρια διάταση παράλληλη στο στρώμα.

 

Πολυστρωματική καμπτική πτυχή.

Η διαφορά ιξωδών μίας πολυστρωματικής  καμπτικής πτυχής μπορεί να είναι  μεγάλη, μεσαία ή μικρή μεταξύ των διαφορετικών στρωμάτων, η οποία όμως επηρεάζει το σχήμα των πτυχών. Η παχύτερη και η σκληρότερη πολυστρωμάτωση τείνει να παράγει, μεγαλύτερα μήκη κυμάτων σε στρογγυλεμένες πτυχές από ότι οι καμπτικές πτυχές απλών σωμάτων. Έτσι οι πολυστρωματικές καμπτικές πτυχές παρουσιάζουν ένα ευρύτερο φάσμα σχημάτων πτυχών από αυτές του απλού στρώματος. Για παράδειγμα και στη φύση και εργαστηριακά, σχηματίζονται πτυχές στρογγυλεμένων αρθρώσεων, γωνιακές οξύληκτες, λοξοζωνικές και συζυγείς.

Επίδραση της ελαστικότητας.

Σε ερευνητικό επίπεδο οι όροι «ελαστικότητα» (με βραχεία χρονική έννοια) και το «έρπον ιξώδες»  (με μακρόχρονη έννοια) περιελήφθησαν στην ανάλυση για την ελαστικο-ιξώδη συμπεριφορά. Για ιδανικά ελαστικά υλικά το επικρατούν μήκος κύματος εκφράζεται σε όρους ελαστικών μονάδων (μέτων) αντίθεσης (Currie et al. 1962) και η εξίσωση (1) Biot Ramberg μπορεί να γραφεί:

 

W_d=2πh(E_L/6E_M)^1/3        (6)

 Όπου E_L και  E_M είναι το μέτρο Young για το στρώμα και το σώμα αντίστοιχα.

(Το μέτρο Young (Ε) ή ελαστικότητας, δεικνύει την εφελκυστική ελαστικότητα ή την τάση που έχει ένα σώμα να παραμορφώνεται κατά μήκος άξονα, όπου στον ίδιο άξονα εφαρμόζονται αντίρροπες δυνάμεις και ισούται με το λόγο παραμόρφωσης προς τάση).

Μία καθαρά ελαστική λύση δεν έχει έννοια σε μόνιμα πτυχωμένα πετρώματα. Το επικρατούν μήκος κύματος, που αναπτύσσεται σε ελαστικό στρώμα εντός ιξώδους σώματος είναι:

 W_d=2πh(G/P)^1/2        (7)

 Όπου G* είναι το μέτρο της ελαστικής διάτμησης του στρώματος και P η παράλληλη προς το στρώμα τάση. Το ιξώδες του περιβάλλοντος σώματος δεν συμμετέχει.

* Το μέτρο ελαστικής διάτμησης (G) είναι μέτρο  που χρησιμοποιούμε για την παραμόρφωση η οποία λαμβάνει χώρα όταν μια δύναμη εφαρμόζεται παράλληλα σε μία πλευρά τεμάχους ενώ από την αντίθετη πλευρά διατηρείται σταθερό από μία άλλη ίση δύναμη.

Όταν στο  δοκίμιο του σχήματος, ύψους L και διατομής Α, εφαρμόζεται στη μία πλευρά δύναμη F, παράλληλη προς τη διατομή, η διατμημημένη πλευρά θα κινηθεί κατά Δ_Χ.

Η διατμητική τάση (shear stress)  καθορίζεται ως το μέγεθος της δύναμης ανά μονάδα της επιφάνειας διατομής που δέχεται τη δύναμη (F/A).  

Η διατμητική παραμόρφωση (shear strain) καθορίζεται ως Δx/L (εγκάρσιο εκτόπισμα).

Το μέτρο ελαστικής διάτμησης G καθορίζεται  ως ο λόγος τάσης προς παραμόρφωση:

G=FL/AΔ_Χ..

ε=στρεβλωτική παραμόρφωση (strain) ορίζεται ως: (l-l₀)/l₀, και ο ρυθμός (ταχύτητα) της παραμόρφωσης ως προς την μονάδα χρόνου (sec):ἐ = dε/dt.)

Ο αδιάστατος λόγος του επικρατούντος μήκος κύματος (R_Wd) μεταξύ ενός ελαστικο-ιξώδους στρώματος, που είναι ενσωματωμένο σε ιξώδες σώμα, δεικνύει την συνδυασμένη συμπεριφορά ελαστικότητας και ιξώδους:

R_Wd= (4 μ_L ἐ /G)^1/2(μ_L/6μ_M)^1/3        (8)

και γράφεται ως  R_Wd= (4 De)^1/2(μ_L/6μ_M)^1/3        (9)

όπου: De= μ_L ἐ /G είναι ο αριθμός Deborah* ο οποίος χρησιμοποιείται για να περιγράψει την ροή μίας ασταθούς  συμπίεσης και αντιπροσωπεύει το ποσό της ελαστικής ενέργειας η οποία αποθηκεύεται η απελευθερώνεται, ή διαφορετικά, το ποσοστό ελαστικότητας ή ιξώδους μιας παραμόρφωσης  Μπορεί ακόμη να θεωρηθεί ο λόγος του χρόνου της χαλάρωσης της τάσης** (stress relaxation time) (μ_L/G) ως προς τον χρόνο της παραμόρφωσης (1/ ἐ).

* ο αριθμός Deborah ή επί το ελληνικότερον «Δεββώρα», προτάθηκε από τον ισραηλινό καθηγητή ρεολογίας Markus Reiner και επέλεξε το όνομα της εν λόγω κυρίας διότι της αποδίδεται η φράση «Τα όρη ρέουν ενώπιόν σου Κύριε», η οποία αναφέρεται στο Έβδομο Βιβλίο της Παλαιάς Διαθήκης (το Βιβλίο των Κριτών) και είναι η μοναδική γυναίκα κριτής – προφήτης της Βίβλου.

** ο χρόνος χαλάρωσης τάσης είναι ιδιότητα υλικού και αντιπροσωπεύει το χρόνο που απαιτείται για να παραμορφωθεί σε ένα συγκεκριμένο όριο μετα από απότομη εφαρμογή  συγκεκριμένου βάρους.

Εάν De>>1, η ανάπαυση τάσης απαιτεί περισσότερο χρόνο από αυτόν της παραμόρφωσης,  η οποία  γίνεται κυρίως ελαστική. Αντιθέτως αν De<<1 η ανάπαυση τάσης είναι ταχύτερη σε σχέση με τη παραμόρφωση, η οποία, σ’ αυτή την περίπτωση, είναι κυρίως ιξώδης.

Ο αριθμός της Δεββώρας δεν είναι κατάλληλος για να δείξει εάν η πτύχωση ενός ελαστικο- ιξώδους στρώματος είναι σαφώς ελαστικό ή ιξώδες, διότι απαιτείται  μια πρόσθετη χρονική παράμετρος, αυτής της καμπυλότητας, όπως καθορίζεται από τον ρυθμό ανάπτυξης. Κατάλληλος λόγος για να προσδιορίσει  αποτελεσματικά την συμπεριφορά της παραμόρφωσης ενός ελαστικο-ιξώδους στρώματος, είναι ο αδιάστατος λόγος R_Wd του ιξώδους, (εξίσωση 8), προς την ελαστικότητα, (εξίσωση 7), του επικρατούντος μήκους κύματος. Αυτός ο λόγος μπορεί να τροποποιηθεί με τη χρήση της σχέσης: P=4μ_Lἐ  και με την υπόθεση ότι η τάση του παράλληλου στρώματος είναι ολοκληρωτικά ιξώδης και ότι μόνο οι καπτικές τάσεις, κατά την διάρκεια της πτύχωσης είναι ελαστικο-ιξώδεις. Τότε:

R_Wd=(G/P)^1/2 (μ_L/6μ_M)^1/3        (10)

Η ανάλυση δείχνει ότι ένα ελαστικο-ιξώδες στρώμα τείνει να είναι ελαστικό αν R_Wd <1 και ιξώδες αν R_Wd>1. Με άλλα λόγια η συμπεριφορά της πτύχωσης του ελαστικο-ιξώδους στρώματος, είναι συγκρίσιμη είτε με  καθαρή ελαστικότητα είτε με καθαρό ιξώδες που εξαρτάται από το πόσο η παραμόρφωση είναι σχετικά γρήγορη ή αργή.

Ως τελικό συμπέρασμα θα λέγαμε ότι η εξίσωση Biot Ramberg ισχύει στις περισσότερες σχετικές γεωλογικές περιπτώσεις.

Ακολουθίες πτυχών (fold trains)

Πειραματικές βραχύνσεις σε μοντέλα στρωμάτων, με υλικά ανάλογα των πετρωμάτων, έδειξαν ότι οι πτυχές οι οποίες σχηματίζονται κατά την διάρκεια συμπίεσης, γενικώς, δεν αναπτύσσονται συγχρόνως. Σχηματίζονται με ένα διαδοχικό τρόπο, είτε η μία μετά την άλλη, όπου η διεύρυνση της μίας πτυχής παρακινεί την εκκίνηση και διεύρυνση της επόμενης είτε σε τυχαίες θέσεις εντός του μοντέλου-υλικού. Γενικά οι πτυχές αναπτύσσονται διαδοχικά και προς τα έξω από τη θέση της αρχικής αστάθειας.

Κάμψεις μεγάλης κλίμακας. Χαρακτηριστικό μήκος κύματος μεγάλης κλίμακας πτυχών.

Κατά τη διάρκεια ανάπτυξης μεγάλης κλίμακας πτυχών, η προς τα πάνω κίνηση ενός καπτώμενου στρώματος σε ένα αντίμορφο ή προς τα κάτω σε ένα σύμμορφο πρέπει να επηρεάζεται από τη βαρύτητα. Αντιλαμβανόμαστε ότι κάτω από την επίδραση της βαρύτητας το αντίμορφο θα έχει την τάση να υποχωρεί και το σύμμορφο θα έχει την τάση να ανυψώνεται. Ως αποτέλεσμα οι καμπτώμενες πτυχές θα έχουν τη τάση να επιπεδοποιούνται, αλλά η παράλληλη προς τα στρώματα συμπίεση αντισταθμίζει αντίθετα αυτή την τάση.

Αν θεωρήσουμε ένα ελαστικό στρώμα πάχους h να επιπλέει σε ένα ιξώδες υπόστρωμα  πυκνότητας ρ και Δσ είναι η διαφορική τάση η οποία σχηματίζει  ελαστικές κάμψεις στο στρώμα, τότε το επικρατούν μήκος κύματος για την κάμψη του ελαστικού στρώματος, κάτω από τη συντονισμένη δράση της δύναμης της βαρύτητας και της πλευρικής διαφορικής τάσης έχουν αναλυτικά υπολογισθεί:

W_d=πh[(2 Δσ)/(hρg)]^1/2                     (11)

Η διαφορική τάση: Δσ = {(Εhρg)/(3(1-υ²)]}^1/2                          (12)

Όπου Ε το μέτρο Young  και υ ο λόγος Poisson* του ελαστικού στρώματος.

Πειραματικά τα αποτελέσματα είχαν αξιοσημείωτη συμφωνία με τη θεωρία. Οι εξισώσεις (10) και (11) δείχνουν ότι απαιτείται μεγάλη συμπιεστική τάση για τον σχηματισμό πτυχών με το μεγαλύτερο μήκος κύματος. Καθώς η διαφορική τάση δεν μπορεί να υπερβεί τη αντοχή του πετρώματος, η εξίσωση (12) θέτει ένα άνω όριο για το μέγεθος των καμπτικών πτυχών.

Ως παράδειγμα, μπορούμε να θεωρήσουμε την περίπτωση κάμψεων του φλοιού. Ένα γρανιτικό πέτρωμα έχει αντοχή (strength) της τάξης των 5.10⁹ dynes cm^-2. Ο μέσος όρος πάχους του φλοιού είναι 30 χλμ. και η μέση πυκνότητά είναι 3gr/cm^-3. Έτσι η μεγαλύτερη τιμή της κάμψης του φλοιού είναι, σύμφωνα με την εξίσωση (11), περίπου 100χλμ.

* ο λόγος Poisson εκφράζει την εγκάρσια συστολική παραμόρφωση (ε_d) προς τη διαμήκη επέκταση της παραμόρφωσης (ε) και ως  προς την κατεύθυνση της επεκτεινόμενης δύναμης:

υ = - ε_d / ε. Η εφελκυστική παραμόρφωση θεωρείται θετική και η συμπιεστική αρνητική. Ο ορισμός του λόγου Poisson  περιλαμβάνει αρνητικό πρόσημο ούτως ώστε τα κανονικά υλικά να έχουν πάντα θετικό λόγο.

Ο λόγος Poisson ενός υλικού επηρεάζει την ταχύτητα διάδοσης και της αντανάκλασης των κυματισμών της τάσης. Στις γεωλογικές εφαρμογές, ο λόγος της συμπίεσης προς την κυματική διατμητική ταχύτητα, η οποία εξαρτάται από τον λόγο Poisson, είναι σημαντικός για να αναγνωρίσουμε τη φύση των πετρωμάτων στα βάθη της Γης. Ακόμη αυτός ο λόγος επηρεάζει την απόσβεση  της τάσης ως προς την απόσταση, σύμφωνα με την αρχή του Saint Venant*, καθώς επίσης και την διανομή της τάσης μεταξύ οπών και ρωγμών.

(* ..η διαφορά μεταξύ των επιδράσεων δύο διαφορετικών αλλά στατικών ισοδύναμων φορτίων μικραίνει σημαντικά σε επαρκώς μεγάλες αποστάσεις από το φορτίο.)

Κύρια σημεία της πτύχωσης από την παραπάνω ανάλυση:

Τρεις φυσικοί μηχανισμοί είναι υπεύθυνοι για την πτύχωση,. Αυτοί είναι η κάμψη, η πλέον βασική, η κυρτότητα και η καμπυλότητα Η ιστορία της μεταμόρφωσης σε κάθε σημείο μίας πτυχής είναι περίπλοκη και οφείλεται στις συνεχείς αλλαγές των συνθηκών τάσης (stress) και στρεβλωτικής παραμόρφωσης (strain). Είναι σημαντικό να σημειωθεί ότι το σχήμα ενός πτυχωμένου στρώματος, από μόνο του, δεν ενεργοποιεί την παραμόρφωση να δράσει σε κάθε σημείο και απαιτούνται επιπρόσθετες πληροφορίες. Οι γνώσεις μας για την ποικιλία των παραμορφώσεων μέσω των πτυχωμένων πετρωμάτων βασίζονται στα αποτελέσματα της ανάλυσης και διανομής της παραμόρφωσης όπως έχει παρατηρηθεί σε αρκετά πειραματικά μοντέλα.

Οι παρακάτω παράγοντες θα πρέπει να λαμβάνονται υπόψη όταν αναλύονται πτυχές σε οποιοδήποτε πέτρωμα:

- Οι ρεολογικές ιδιότητες των παραμορφωμένων υλικών.

- Η μηχανική ανισοτροπία της μάζας του πετρώματος.

- Το πεδίο τάσεων που δρα στο πέτρωμα συμπεριλαμβανομένων των δυνάμεων που ασκούνται από το βάρος του σώματος.

- Η επίδραση οποιασδήποτε ετερογένειας.

- Οι συνθήκες των περιθωρίων.

 

Β. Ανδρώνης

 

Αναφορές

Richard H.Groshong, Jr.: 3-D Structural Geology, A Practical Guide to Quantitative Surface and Subsurface Map Interpretation. Second Edition Springer ISBN-13 978-3-540-31054-9 Berlin Heidelberg New York.

Fusseis, F. (Freie Universität Berlin), and Grasemann, B.(Institut für Geologie, University of Vienna) 2002:  Animation of refold structures. In: (Ed.) Andy Bobyarchick, Visualization, Teaching and Learning in Structural Geology, Journal of the Virtual Explorer, Electronic Edition, ISSN 1441-8142, volume 9, paper 1.

Krystof Verner: The Mapping of Geological Structures Czech Geological Survey in Prague.

Thiessen, R. L. 1986: Two-dimensional refold interference patterns. J. Struct. Geol. 8:563–573.

Thiessen, R. L. and Means W. D. 1980: Classification of fold interference patterns: a re-examination. Journal of Structural Geology 2, 311-326.

Bernhard Grasemann, G. Wiesmayr, E. Draganits and F. Fusseis: Classification of Refold Structures: Department of Geological Sciences, University of Vienna, A-1090 Vienna, Austria.

O’Driscoll, E. S: 1962. Experimental patterns in superimposed similar folding. J. Alberta Soc. Petrol. Geol. 10:145–167.

Neville J. Price, John W. Cosgrove: Analysis of Geological Structures, Cambridge University Press

Arvind Johnson: Styles Of Folding Mechanics And Mechanisms Of Folding Of Natural Elastic Materials  (Stanford University), Elsevier Publishing Company, Amsterdam, Oxford, New York, 1977.

Stefan M. Schmalholz: Scaled amplification equation: A key to the folding history of buckled viscous single-layers. Geological Institut, ETH Zurich, 8092 Zurich, Switzerland

Peter J. Hudleston Department of Geology and Geophysics, University of Minnesota, Minneapolis, MN and Susan H. Treagus School of Earth, Atmospheric and Environmental Sciences, University of Manchester: Information from folds: A review.

Ramsay J.G. & Huber M.I. – 1987: The techniques of modern structural geology - Volume2 : Folds and fractures. Academic Press, London

Ashok Kumar Dubey: Understanding an Orogenic Belt: Structural Evolution of the Himalaya.

Hemin A. Koyi, Neil S. Mancktelow: Tectonic Modeling: A Volume in Honor of Hans Ramberg, Issue 193, 2001.

Biot, M.A., 1965a.: Mechanics of Incremental Deformations. John Wiley and Sons, New York.

Gilbert Wilson:  Introduction to Small scale Geological Structures, Springer, Dordrecht.

Kaj M. Johnson, Arvid M. Johnson: Mechanical analysis of the geometry of forced-folds.

G.K. Gilbert: Geomechanics Laboratory, Earth and Atmospheric Sciences, Purdue University, 1397 CIVL, West Lafayette, IN 47907, USA.

Johnson, A.M., Pfaff, V.J., 1989: Parallel, similar and constrained folds. Engineering Geology 27, 115e180.

Roderic Lakes: University of Wisconsin, Distinguished Professor, Department of Engineering Physics, Rheology Research Center: Viscoelasticity.

J. W. Cosgrove E: The association of folds and fractures and the link between folding, fracturing and fluid flow during the evolution of a fold–thrust belt: A brief review.  Department of Earth Science & Engineering, Imperial College, London

Stefan M. Schmalholz, Yuri Yu. Podladchikov: Strain and competence contrast estimation from fold shape. Geologisches Institut, ETH Zentrum, 8092 Zurich, Switzerland. Tectonophysics 340 (2001) 195–213

D. W. Schmid and Yu. Y. Podladchikov: Fold amplification rates and dominant wavelength selection in multilayer stacks. Physics of Geological Processes, University of Oslo, Oslo, Norway. Philosophical Magazine, Vol. 86, Nos. 21–22, 21 July–1 August 2006, 3409–3423

Stefan M. Schmalholz(1) & Daniel W. Schmid(2): Folding in power-law viscous multi-layers

(1) Institute of Geology and Palaeontology, University of Lausanne, Switzerland

(2) Physics of Geological Processes, University of Oslo, Norway, Phil. Trans. R. Soc. A (2012) 370.

Hans Ramberg: Evolution of ptygmatic folding (University of Chicago), Norsk Geologisk  Tidsskrift 39 1959

Xiaolong Liu: Numerical simulation of viscoelastic buckle folds: Implications for stress, fractures, porosity and fluid flow. Department of Geosciences and Geological and Petroleum Engineering Missouri University of Science and Technology.

Mohammed S. Ameen, John W. Cosgrove: Forced Folds and Fractures.

Geological Society, Special Publication No169

N.C.Bobillo-AresaF.BastidabJ.Allerb On tangential longitudinal strain folding

Tectonophysics Volume 319, Issue 1, 15 March 2000, Pages 53-68